

We would first begin with a game called "The Spinning wheel"
This will give the students a good idea of how to think about randomness.
Introduce the Law of Large Numbers
Draw independent observations at random from any population with finite mean m. Decide how accurately you would like to estimate m. As the number of observations drawn increases, the mean x-bar of the observed values eventually approaches the mean m of the population as closely as you specified and then stays that close.
Make a connection to the game. Have the students calculate what the mean would be for that population, and let them discover that as they take more and more trials that the mean will come as close as they want.
Begin by defining what a sample space and an event is and moving into the probability of an event.
Next we will move into discussing independence and basic operation rules for computing event probabilities.
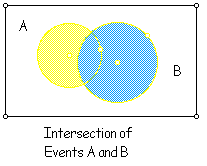
Follow by discussing the intersection, union and complement of events.



Begin by doing the classic coin toss experiment.
Discuss the difinitions of a random variable and what it means to be desrete (takes on numercial values) or continuous (values that take on certain intervals).
Talk about Discrtete Probability Distributions and relate to the game from the beginning.
Since this is a normal distribution make the connection to Normal distributions (which resemble the bell shaped curves that were discussed earlier in the semester.)
Move on to The Binomial Distribution and the Geometric Distribution.