

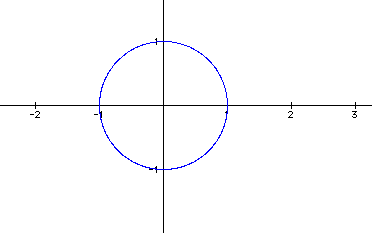
A Polar Equation is a curve with variables r and theta. Theta represents the angle of rotation and r is the radius, creating a set of coordinates (r, theta). For instance, the polar equation r=1 represents the unit circle, since the radius is 1 for all angles of theta. See graph of r=1, 0<=theta<=2Pi below.
Consider the polar equation:
The graph below shows the graph when n=1.
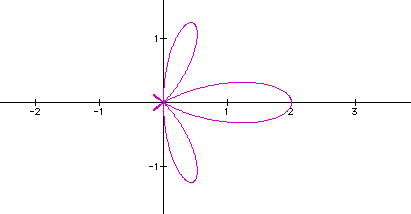
Notice the graph has x-axis symmetry and the shape looks like a leaf. What happens as we vary n? The graph below shows a family of curves with n=-5, n=-3, n=-1 and n=0.
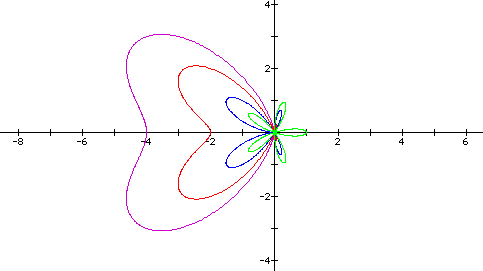
Notice when n=-5 and n=-3, the shape of the graph is a heart. When n=-1, the shape is like a butterfly and when n=0, we get a rose with 5 petals. All curves above are symmetric with respect to the x-axis.
The graph below shows a family of curves with n=5, n=3, n=1 and n=0.
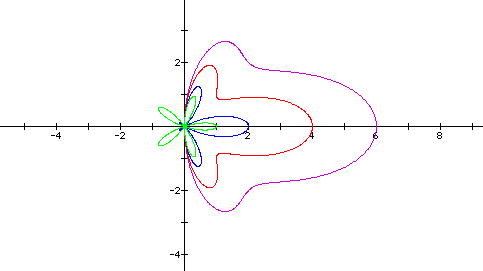
Notice that for positive n we are not getting the same shape on the right side of the y-axis. When n=0 we get a rose graph, when n=1 we get a leaf with three petals, and with n=3 and n=5, we get a bell shape. At what value of n does the graph become this bell. Below is a family of graphs with n ranging from -5 to 5.
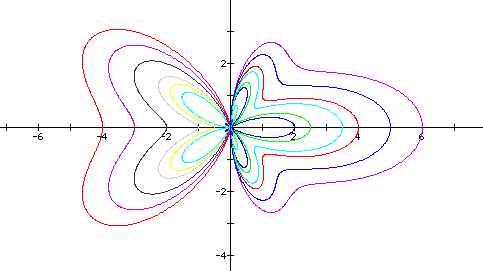
We can see that if the value of n is negative the graph becomes more heart like, while if the value of n is positive, the graph becomes more bell like. As |n| increases, the graph stretches both horizontally and vertically.
What happens as we vary n from -10 to 10?
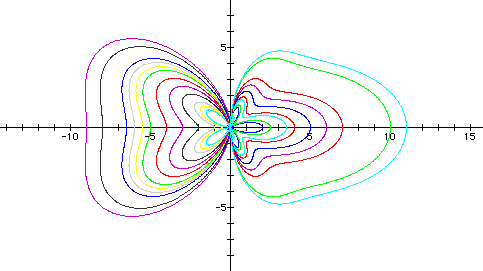
Essentially, it appears that the graphs continue to stretch. As n gets more and more negative, the graph becomes less heart like, and as the values of n become more positive, the curves become less bell like. The "perfect heart" appears to occur when n=-5, and the "perfect bell" appears to occur when n=5.