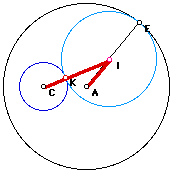

To prove that the path of the center of the tangent circle is an elipse, we need to show that the sum of the distance from I to two fixed points is a constant. Notice that C and A are two fixed points because they are the centers of the two original circles. Notice that AE is the radius of the larger circle A, and CK is the radius of the small circle C. IK and IE are both radii of the tangent circle. Thus, IK = IE. Since AE = AI + IE, by the segment addition postulate, we can say that AE = AI + IK, by substitution. We can also observe that the distance from the center of the tangent circle to the center of the small circle is IC = IK + KC, again by segment addition. Therefore, we can say that IA + IC = CK + AE, by substitution. This means that the sum of the distance of the center of the tangent circle to point A and the distance from the center of the tangent circle to point C is always equal to the sum of the radii of the two original circles, which remain fixed. So, The path of point I is an elipse as point E is moved around the large circle.