
Write Up # 9
Pedal Triangles
by: Angel R. Abney
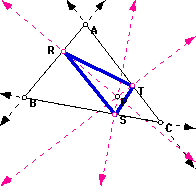
Let Triangle ABC be any triangle. then if P is any point in the plane, the triangle formed by locating three points R, S, and T that are the intersections of the constructed perpendiculars to the sides of ABC(extended) is called the Pedal Triangle for Pedal Point P.

To construct the Pedal Triangle, draw triangle ABC and point P is any point in the plane (See picture above). Then construct the perpendiculars to sides AB, AC, and BC from the point P. The intersections of the perpendiculars and the sides are points R, S, T. the thick blue triangle below is the Pedal Triangle, and P is the Pedal Point.
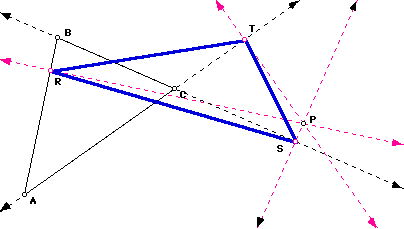
To manipulate the construction of the Pedal Triangle, click on Pedal script. You must have GSP in order to run the script. Select Points ABC and P, then press play on the script. You can then move the Pedal point, P around to see how this affects the Pedal triangle.
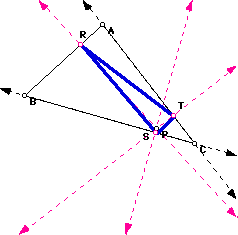
Notice, that as P is moved to the side of triangle ABC, P becomes one of the vertices of triangle RST (see picture above). If P is moved to line BC, then P is concurrent with S. If P is moved to line AC, P lies on the same point as T, and if P is moved to line AB, P is concurrent with R.
Observations:
1. If P is moved to the sides (even extended sides) of triangle ABC, then P becomes one of the vertices of the Pedal Triangle see picture above. Click here to see proof.
2. If P is inside of triangle ABC and triangle ABC is acute, then the vertices of the Pedal Triangle lie on segments BC, AB, and AC.
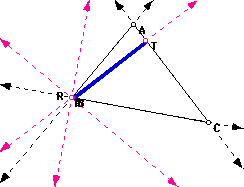
3. If P lies on a vertex of triangle ABC, then P coexist with two vertices of the Pedal triangle as well. Thus, Triangle RST becomes a segment. In other words, it is a degenerate triangle. This line segment is called the Simpson's Line
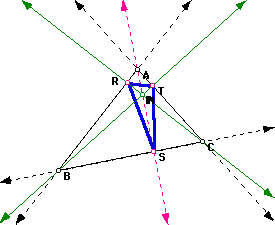
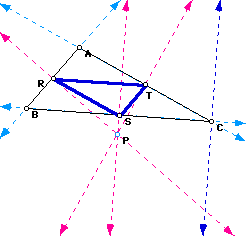
4. If P is the orthocenter (intersection of altitudes) of triangle ABC, then R, S, and T lie on the intersection of the altitudes and the sides of the triangle. If the orthocenter lies outside of triangle ABC, then two of the points of the Pedal triangle lie on the extended sides of triangle ABC (see second picture below).
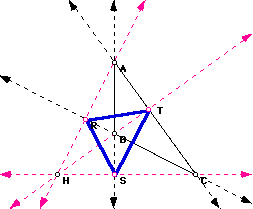
5. If triangle ABC is a right triangle, and P lies on the side opposite the right angle, then triangle RTS is a right triangle. Click here to see proof.
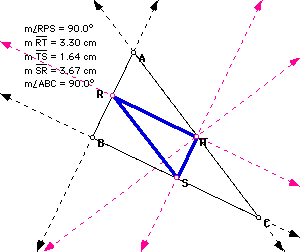
6. If triangle ABC is a right triangle, then angle RPS is always a right angle and line RP is parallel to line BC.
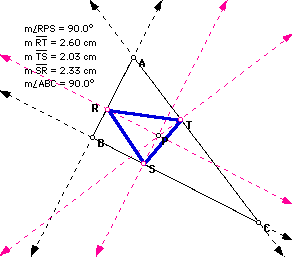
7. If the Pedal point is the In-center (intersection of the angle bisectors), then points R, S, and T always lie on the non-extended sides of triangle ABC, since the in-center is always inside of triangle ABC.
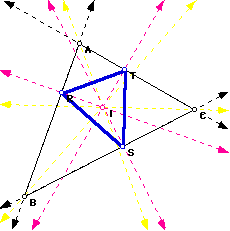
8. It appears that the measure of angle ABC is either equal to the measure of angle RPS, or that angle ABC and angle RPS are supplementary.
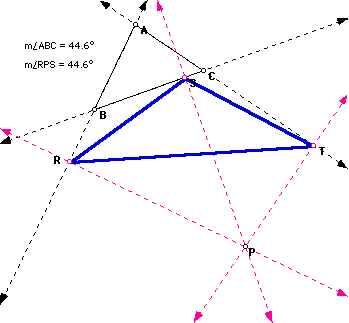
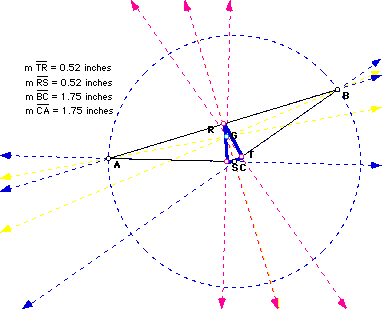
9. If P is the circumcenter ( intersection of perpendicular bisectors), and triangle ABC is a right triangle, then P will lie on point R. Thus, triangle RST will also be a right triangle.
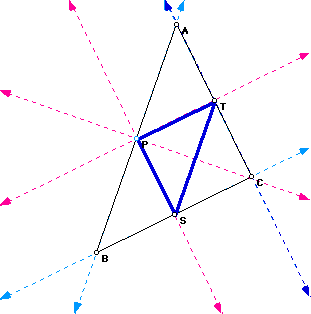
10. If P is the circumcenter, triangle RST is inscribed in triangle ABC (even if P is outside of triangle ABC).
11. It should be obvious that if P is the circumcenter, then points R, S, and T lie on the intersection of the perpendicular bisectors and segments AB, BC, and AC. Therefore, R, S, and T are always the mid-points of segments AB, BC, and AC, respectively.
12. If P is the circumcenter, then the sides of the Pedal triangle are parallel to the sides of triangle ABC.
13. If P is the centroid (intersection of the medians) of triangle ABC and triangle ABC is isoceles, then the pedal triangle is also isoceles.