

The function, ![]() , is a parabola in
standard form with zeros:
, is a parabola in
standard form with zeros:
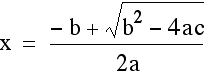 and
and
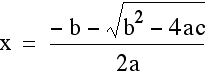 .
.If we are interested in the location of the zeros of this function, the standard form of a parabola above is very useful. I am more interested in transformations of parabolas. In this case, I feel that vertex form is more appropriate. To see conversion from standard form to vertex form, click here.
Now I will explore the effects of changing the parameters a, h, and k. First I will examine the effects of varying h with fixed values for a and k. Let a = k = 1. Below are the graphs of
with h = -5, -3, -1, 0, 2, 4, 6. The colors of the values of h correspond to the same color on the graph.
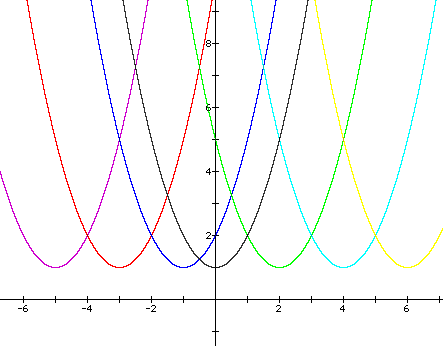
Notice that varying h causes horizontal translations. Subtracting negative values, or in effect adding a constant to the x, inside the parentheses, causes the parabola to shift left along the x-axis. Subracting positive constants causes a horizotal shift to the right. Observe that the shift occurs in the opposite direction of the sign of the constant being added to x. When h<0, the vertex shifts to the left of the y-axis. When h>0, the vertex shifts to the right of the y-axis, and when h=0, the vertex lies on the y-axis.
Now I will examine the effects of varying k with fixed values of a and h. Let a=h=1. Below are the graphs of
with k = -5, -3, -1, 0, 2, 4, 6. The colors of the values of k correspond to the same color on the graph.
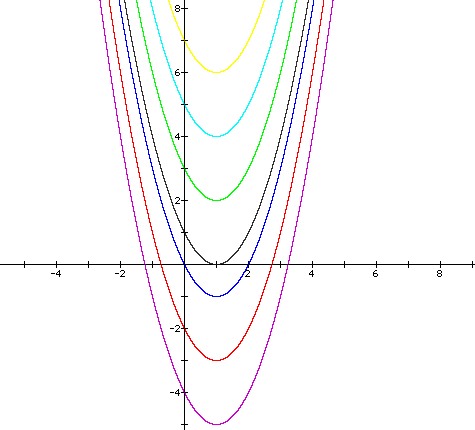
Varying the values of k causes vertical translations. Notice that as the value of k increases, the vertex of the parabola shifts vertically in the positive direction. When k is negative, the graph shifts below the x-axis, and when k is positive, the graph shifts above the x-axis. When k=0, the vertex lies on the x-axis.
It is clear that varying h and k cause rigid transformations, where the graph actually moves. Will varying the last parameter, a, also create a rigid transformation? Again, we will fix the values of h and k and vary the parameter a. Below are the graphs of
with a= -3, -1, 0, 2, 4. The colors of the values of k correspond to the same color on the graph.
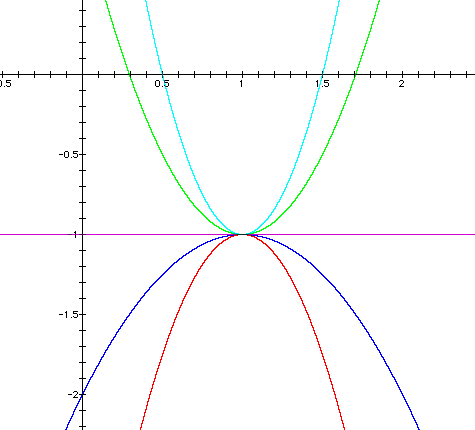
Notice that varying the value of a creates
a nonrigid transformation. The vertex remains in the same place,
while the parabola is widened, steepened or flipped. When a<0,
the parabola opens down. When a>0, the parabola opens up, and
when a=0, the quadratic term goes away. Therefore, the graph is
no longer a parabola, but it is a horizontal line. Observe, also,
that the greater ![]() , the steeper the
parabola.
, the steeper the
parabola.