Double Wedding Ring
*442

Analysis of Double Wedding Ring
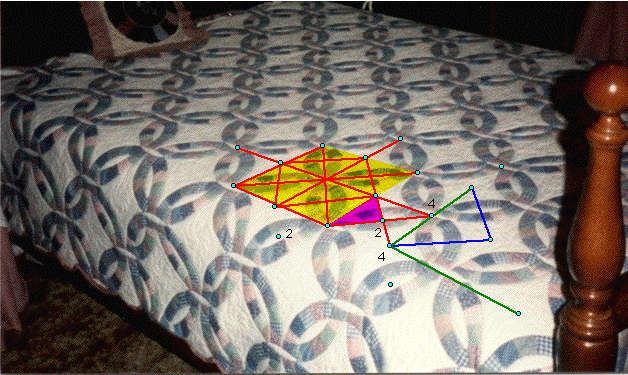
KEY:
1) red segments represent reflection mirrors
2) light green segments represent glide mirrors that are not reflection mirrors
3) dark blue segments represent translation generators
4) dark green segments represent shortest glide vectors that are not translation
generators
5) yellow points represent cyclic centers
6) light blue points represent dihedral centers
7) fundamental region is shaded pink
8) quilt block is shaded yellow
Symmetries present:
reflection, glide reflection, rotation, translation
Description of symmetries: There
are vertical, horizontal, and diagonal reflection mirrors at 45 degree angles
as shown. These mirrors are also glide mirrors. 4-fold dihedral rotation centers
are located at the intersection of four mirror lines. 2-fold dihedral rotation
centers are located at the intersection of two diagonal mirror lines. The
shortest translation vectors are twice the distance between the diagonal mirrors.
The shortest glide vectors horizontally and vertically are twice the distance
between the horizontal and vertical mirrors.
Description of fundamental region:
The fundamental region is a 45-45-90 right triangle.
Description of symmetries in block: Technically,
this quilt does not have blocks as it was purchased with the pattern printed
on it. However, this quilt can be hand-pieced and a block would have *4 symmetry.
Relationship between block and fundamental region:
A block is approximately 16 fundamental regions.
Description of symmetries in quilting:
The quilter 'traced' the pattern of the quilt, embellishing it by quilting
a flower design in the center of the 'circles'. Thus, the quilting symmetry
is not in harmony with the quilt symmetry. For an analysis of the quilted
flower design, see below.
Double Wedding Ring Quilted Block
Pattern
To see entire quilt, scroll up to the top.
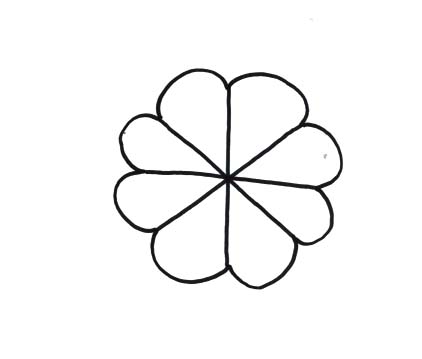
Analysis of hand-quilted flower
This hand-quilted element of the quilt would
have cyclic 8 symmetry if analyzed individually. (Note that the above drawing
is intended to illustrate congruent petals.)


