Write-up # 10
Explorations with Parametric Curves
by
Holly Anthony
Problem: Graph the following equations and change the equations to explore other graphs.
![]()
After this investigation, I will explore the equations:
![]()
Let's begin by graphing these two equations.
![]()
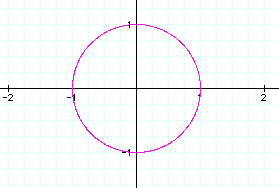
Notice that the graph is a circle with its center at (0,0) and a radius of 1. Let's alter these equations and investigate the effects of our alterations.
Let's begin with the equations written so that they are in the form:
![]()
and investigate them for different values of a and b.
First, let's look at when a = b.
|
a = b = 1
|
purple
|
|
a = b = 2
|
blue
|
|
a = b = 5
|
green
|
|
a = b = -2
|
blue
|
|
a = b = -5
|
green
|
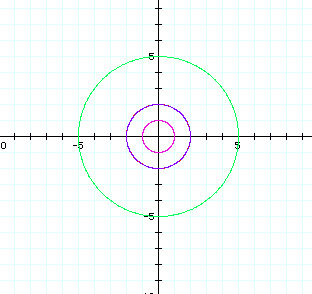
Notice that the graphs are all circles. Each graph has its center at (0,0). Also notice, that the graph when a = b = 2 is the same as the graph when a = b = -2. Therefore, putting a negative in front of a and b in the equation does not give a different graph than when a and b are positive. Also, notice that the radius of each circle is the absolute value of a and/or b. (The graph crosses the x-axis and the y-axis at +/- a and +/- b.)
From this, I conclude that when a = b:
Now, let's look at when a < b.
|
a = 1 < b = 2 |
red
|
|
a = 2 < b = 3
|
purple
|
|
a = 4 < b = 5
|
blue
|
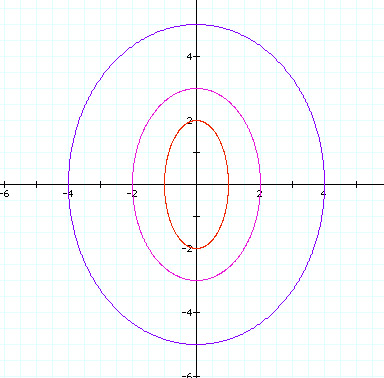
Notice the we get three ellipses. Each crosses the x-axis at +/- a and the y-axis at +/- b and has its center at (0,0). The major axis lies on the y-axis and the minor axis lies on the x-axis.
Let's see if this is true if I include negative numbers in my investigation.
|
a = -3 < b = 1
|
red
|
|
a = -2 < b = 2
|
purple
|
|
a = -1 < b = 3
|
green
|
|
a = 1 < b = 5
|
blue
|
Notice how our graph has changed. We still have ellipses with their centers at (0,0) except for the purple graph. The purple graph represents when a = -2 and b = 2 and although -2 < 2, we know that their absolute values are equal, so this graph is a circle.
Also, notice that the ellipses do not all have major axes on the y-axis and minor axes on the x-axis. The negative numbers seem to be affecting this fact. I know that a < b, but I also realize that the absolute value of a is greater than the absolute value of b in some of our cases, thus changing the location of its major and minor axes. So, I will conclude:
Finally, let's look at when a > b.
|
a = 2 > b = 1
|
red
|
|
a = 4 > b = 3
|
purple
|
|
a = 6 > b = 5
|
blue
|
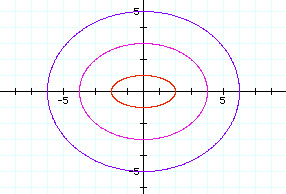
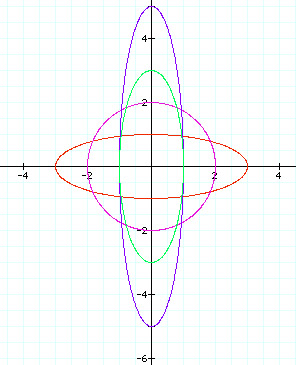
Let's examine this graph. Notice the we get three ellipses. Each crosses the x-axis at +/- a and the y-axis at +/- b and has its center at (0,0). The major axis lies on the x-axis and the minor axis lies on the y-axis. (This appears to be opposite of the case when a < b.)
Will we have the same situation when negatives are included?
|
a = 1 > b = -3
|
red
|
|
a = 2 > b = -2
|
purple
|
|
a = 5 > b= 1
|
blue
|
|
a = 3 > b = -1
|
green
|
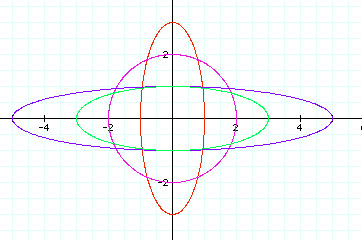
Notice how our graph has changed. We still have ellipses with their centers at (0,0) except for the purple graph. The purple graph represents when a = 2 and b = -2 and although 2 > -2, we know that their absolute values are equal, so this graph is a circle.
Also, notice that the ellipses do not all have major axes on the x-axis and minor axes on the y-axis. The negative numbers are again affecting this fact. I know that a > b, but I also realize that the absolute value of a is less than the absolute value of b in some of our cases, thus changing the location of its major and minor axes. So, I will conclude:
Finally, let's alter the equations so they are in the form:
![]()
and see what is changed when h is any real number.
We will investigate with graphs for small -3 < h < 3.
First, let's look at when a = b.
When a = b = 2 and we vary 'h'.
|
h = 2
|
teal
|
|
h = 1
|
green
|
|
h = 0
|
blue
|
|
h = -1
|
purple
|
|
h = -2
|
red
|
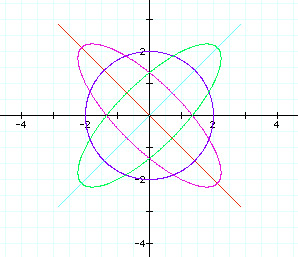
Let's examine this graph. Notice that we get circles, lines, and ellipses as 'h' varies. The circle and ellipses are centered at the origin. Also, notice that when 'h' was negative, the ellipses had a major axis with a negative slope and when 'h' was positive, the ellipses had a major axis with a positive slope
Other observations that I make include that when h = 0, the graph is a circle and that when the absolute value of h equals either a or b, the parametric equation graphs a line.
Now, let's look at when a < b.
When a = 3 < b = 5 and we vary 'h'.
|
h = 2
|
teal
|
|
h = 1
|
green
|
|
h = 0
|
blue
|
|
h = -1
|
purple
|
|
h = -2
|
red
|
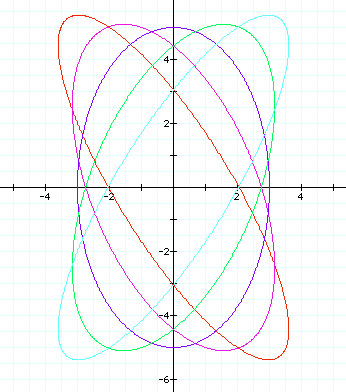
Notice that the graphs are all ellipses with center at (0,0). Like above, when 'h' is negative, the ellipse has a major axis with a negative slope and when'h' is positive, the ellipse has a major axis with a positive slope, and when h = 0, the ellipse has a major axis along the y-axis.
Finally, let's look at when a > b.
When a = 5 > b = 2 and we vary 'h'.
|
h = 2
|
teal
|
|
h = 1
|
green
|
|
h = 0
|
blue
|
|
h = -1
|
purple
|
|
h = -2
|
red
|
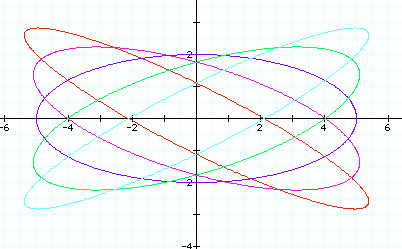
Upon examination of this graph, I conclude that the same properties hold true for it as when a < b, except that when h = 0, the ellipse has a major axis along the x-axis instead of the y-axis as before.