
Write-up #7
Explorations with Tangent Circles
by
Holly Anthony
A Summary of My Experience With this Investigation
In this investigation, I will proceed through the problem presented and then summarize my experience and frustrations with this investigation.
Problem: Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point.
First, we are given two circles A and C, and a point E on A. Our goal is to construct a circle tangent to both circle A and C, with one point of tangency being designated, in this case, E.

Second, construct a line through center A and point E. (The center of the tangent circle must lie on this line.) Then, construct a circle with center E and radius equal to circle C. (The radius is EG)
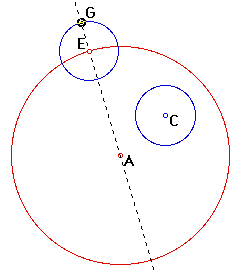
Since the center of the tangent circle must be equidistant from point E and circle C, then if we extend the segments by a distance equal to radius C, the center of the tangent circle must also be equidistant from point G and center C.
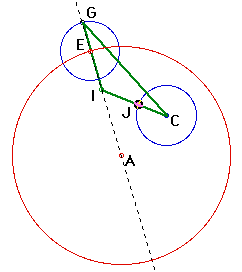
Next, connect point C and point G. (This will be the base of the isosceles triangle.) Then construct a perpendicular bisector through the midpoint of GC. The third vertex of the isosceles triangle is where the two constructed lines intersect. This point is also the center of the tangent circle.
Finally, construct a circle with center I and radius IE. The black circle below is the circle we constructed to be tangent to both circle A and C as well as point E.
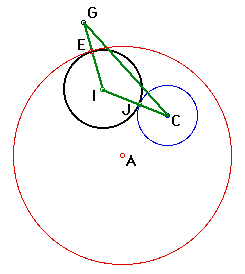
For a script to construct this tangent circle, open GSP and click here.
To explore the graph above with the isosceles triangle shown, open GSP and click here.
As point E moves around Circle A, the locus of the center of the tangent circle I traces out an ellipse (shown in light green).
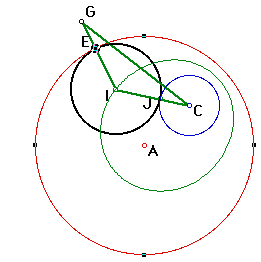
To animate the graph and see the ellipse traced for yourself, open GSP and click here.
The foci of the ellipse are located at the centers of the given circle A and C.
The two sides of the isosceles triangle IG and IC are equal in length by definition. Therefore, the distance from center I to center C plus the distance from center I to center A is the same as the sum of the radii of the given circles A and C.
This is the definition of the foci of an ellipse.
The tangent circle investigation has lots of other topics to offer such as explorations with ellipses and hyperbolas. I have only touched the surface of the topics that could be explored here.
To explore this construction for other possibilities, click here.
A cool exploration involves constructing a line tangent to the ellipse through point I and tracing this line as the tangent point of the constructed circle moves around the large circle. This envelope of lines produced are essential to the underlying technique of folding wax paper to define an ellipse by the envelope of folds.
A Brief Summary of My Experience and Frustrations with this Investigation
At first, this investigation was trying to my patience as I had trouble with animation and tracing in GSP. However, the more I explored and investigated this problem, the more fun it became. I have discovered that this problem can offer a wide range of mathematical exploration for students... too much to mention in this write-up!) The experience was worth the frustration!