Write-up # 9
Explorations with Pedal Triangles
by
Holly Anthony
Problem:
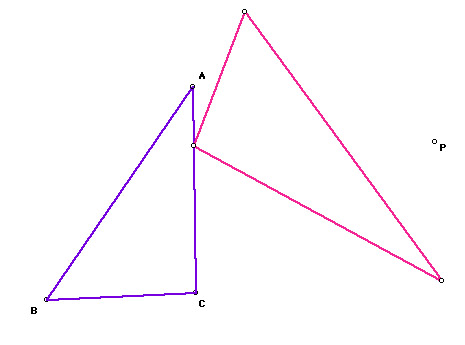
Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) will locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
Let's look at the graph of the situation described above.

Triangle ABC is blue and the Pedal Triangle is pink.
To play with these triangles, open GSP and click here.
Using Geometer's Sketchpad, I created a script for the general construction of a pedal triangle to triangle ABC where P is any point in the plane of ABC.
To play the script, open GSP and click here.
Explorations
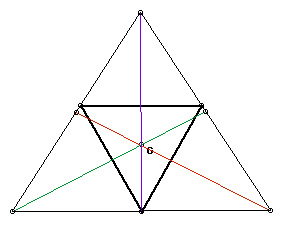
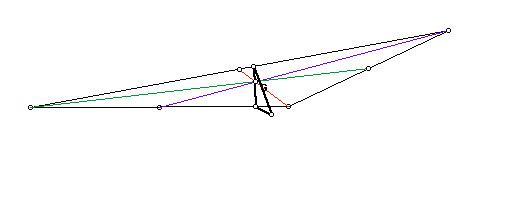
What if pedal point P is the centroid of triangle ABC?
To explore this question for yourself, open GSP and click here.
Let's look at various cases.
In the following pictures, the pedal triangle will be the bold-faced triangle.
Acute
Obtuse
Right
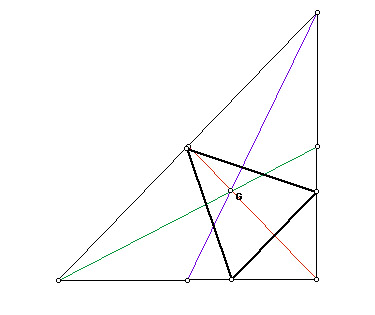
I found that when the centroid is the pedal point, the pedal triangle is constructed inside triangle ABC and remains inside triangle ABC when it is acute and right. However, I discovered that when triangle ABC is obtuse, one vertex of the pedal triangle will move outside of triangle ABC.
I found no relation between area of triangle ABC and the pedal triangle.
To manipulate the graph for yourself with area being calculated, open GSP and click here.
What if pedal point P is the incenter of triangle ABC?
To explore this question for yourself, open GSP and click here.
Let's explore this question.
In the following picture, the pedal triangle will be green.
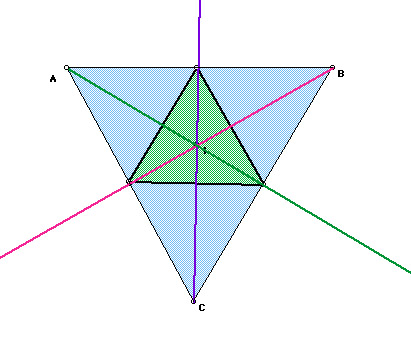
I again found that the pedal triangle is constructed inside triangle ABC and that it remains inside regardless of how you manipulate the graph. However, it is important to note that as triangle ABC becomes more obtuse, the pedal triangle almost becomes a line.
I did not find a relation between the area of triangle ABC and the pedal triangle.
What if pedal point P is the orthocenter of triangle ABC?
To explore this question for yourself, open GSP and click here.
Let's explore the various cases.
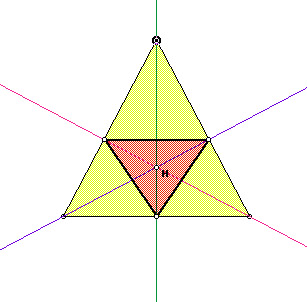
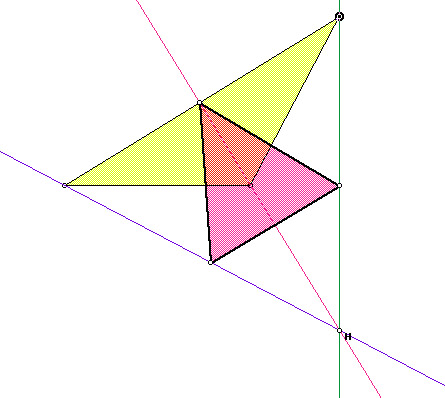
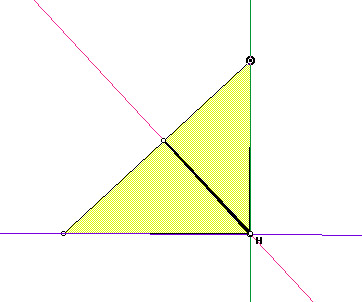
In the following picture, the pedal triangle will be pink.
Acute
Obtuse
Right
In this exploration, I found that when the orthocenter is the pedal point, the triangle is formed inside triangle ABC. However, when manipulating the graph, various situations occur. From observing acute, obtuse, and right triangles, I conclude:
I did not find any relation between area of the pedal triangle and area of triangle ABC.
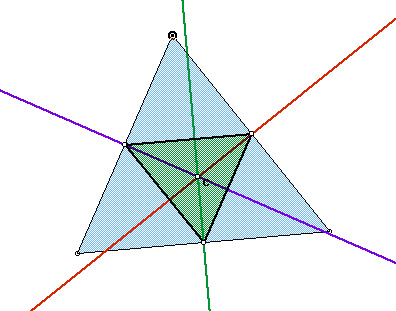
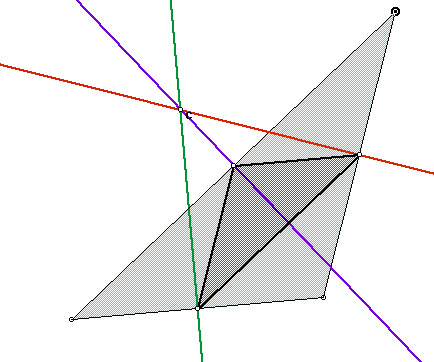
What if pedal point P is the circumcenter of triangle ABC?
To explore this question for yourself, open GSP and click here.
Let's explore the various cases.
In the following picture, the pedal triangle will be green.
Acute
Obtuse
Right
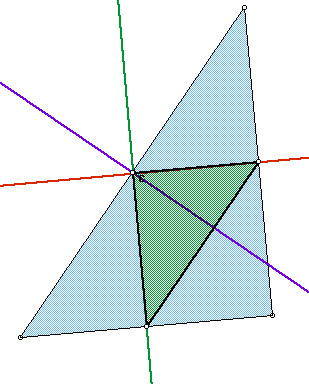
In this exploration, I found that when the circumcenter is the pedal point, the triangle is formed inside triangle ABC. However, when manipulating the graph, various situations occur. From observing acute, obtuse, and right triangles, I conclude:
I also discovered a relation between area of the pedal triangle and area of triangle ABC. The area of the pedal triangle is 1/4 the area of triangle ABC. To manipulate the graph for yourself with area being calculated, open GSP and click here.
Extensions of this Problem
What if pedal point P is the center of the nine point circle for triangle ABC?
What if pedal point P is on a side of the triangle?
What if pedal point P is one of the vertices of triangle ABC?