Start with the following expression and its graph:
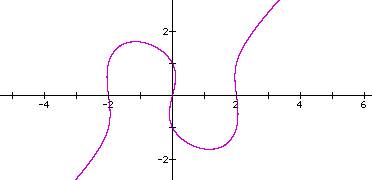
To first explore this graph, look at the following expression with varied values of n.
![]()
n=4, n=2, n=1, n=0.01, n=-3
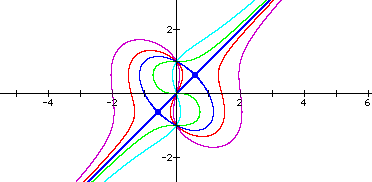
As n takes on smaller values, such as -40, -400, etc., the graph appears to merge with the y-axis....but actually is just becoming larger. Check it out!
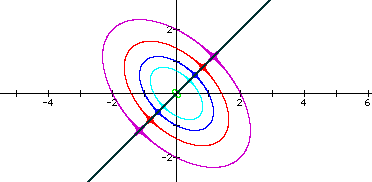
Examining the graph such that ![]()
yeids the graph of y=x, with an added bisected ellipse. y=x are obvious solutions to the equation since x^3-nx=x^3-nx. The added ellipse must take into account the solutions from the cubed terms. As n approaches zero, the ellipse gets smaller. For any negative values of n, the only real solutions are those when y=x; therefore, no ellipse exists on those graphs.
n=4, n=2, n=1, n=0.5, n=0.01
Back to the original equation at the top of the page, changing the x-squared term to (x-0.8)^2, will modify the curve to the left of the y-axis (red). Modifying the y-squared term the same way, will not only alter the curve to the right of the y-axis, but raise the graph (blue).
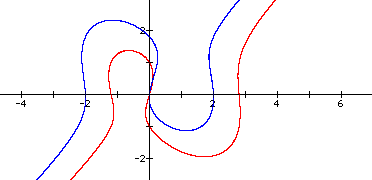
As with any shift along the x-axis, to move the graph 0.5 to
the left, ALL x terms must be changed by +0.5. Which yeilds the
final expression,![]()
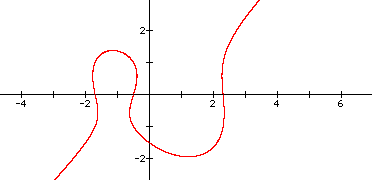
Adding a constant to the y-side (or subtracting one from the x-side) will change the curve as follows:
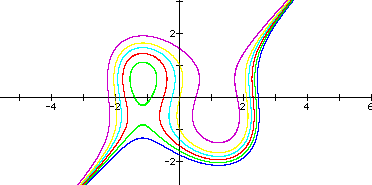
n=2, n=1, n=0, n=-1, n=-2, n=-4
Click here to see the expression taken to the THIRD DIMENSION!!