Using the formula function on spreadsheet programs, tables of values can be created and graphed almost like a graphing calculator.
Consider the graphs of x=cos(at) and y=sin(bt) for t in the interval [ 0, 2pi].
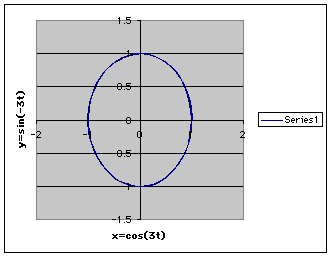
The following is a parametric graph of x=cos(3t) and y=sin(-3t) for the values of t in the interval [0,2pi]. Since the formula calculator did not seem to recognize "pi," I used the typical 3.14. In the first column (column A), I begin with t=0 and increment it by 0.05pi for each point. This makes a total locus of 41 points between zero and 2pi. Column B is the x-coordinate and column C is the y-coordinate. To see the spreadsheet, click HERE.

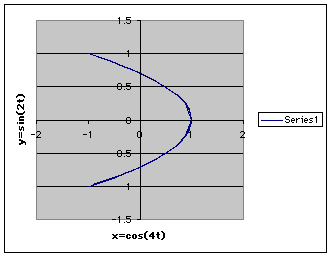
Notice the image makes a circle of radius = 1. Every graph created where the absolute value of a was equal to the absolute value of b, a circle of radius one was generated The next image is x=cos(4t) and y=sin(2t). Instead of a circle, this time we get another conic--a parabola.
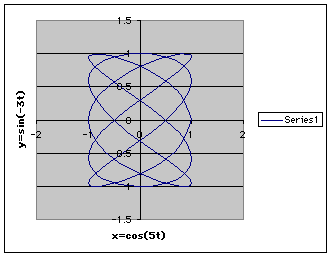
With a smaller increment of t, the curve would be smoother, due to smaller spaces between the plotted points. As the absolute value of a increases, the graph becomes more and more complex. It appears to have a greater number of cycles. The following is a graph with a=5. If a =-5, the graph is exactly the same. This is because cos(-x) =cos (x).
To see an image of a=10, click HERE.
Earlier when a=4, the parabola was simply just one cycle, or maybe even half a cycle of what occurs with greater values of a.
Again, the graphs above were all done with 40 increments between 0 and 2pi. What if smaller increments are used? Like increments of 0.005pi (401 points)? In the following image, 401 points are graphed of x=cos(5 t) and y=sin(-3 t). This image is exactly the same when only 41 points had been graphed.

The increments did not seem to matter so much on the spreadsheet, but when graphing on the TI-83 graphing calculator, it made a large difference. For instance when, x=cos(20t) and y=cos(20t) are graphed with increments of approximately 0.3, a (really pretty) star pattern is formed. Changing the increments to 0.005pi, however, revealed the original discovery I found on the spreadsheet--the (more accurate) circle with radius of 1.