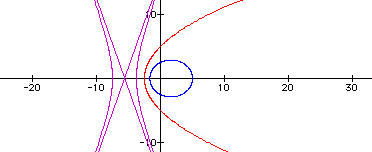
Conics! The best part of algebra has been brought to a polar existence. By varying the eccentricity (k) in the following equations, familiar friends come to life.
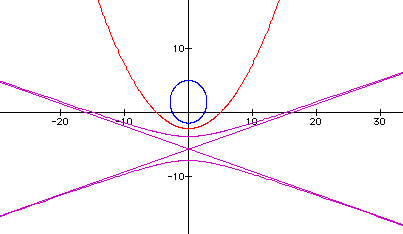
Starting with r=5k/[1-kcos(theta)], the eccentricity is varied and three conics are formed.
k=3 (hyperbola)
k=1 (parabola)
k=0.5 (ellipse)

Changing the coefficient of k in the numerator (referred to as p), the hyperbola shifts and expands/contracts. As p approaches zero, the hyperbola approaches the assymptotes.
p=-10, p=-5, p=0.5, p=5, p=10
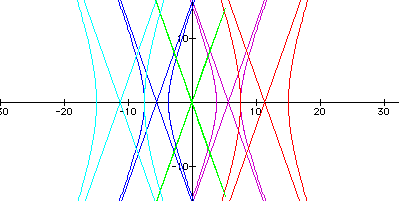
A similar effect happens to the parabola and ellipse when p is varied. As the absolute value of p gets larger the parabola becomes wider. A negative sign also changes the direction--the parabola then opens to the left.
p=-10, p=-5, p=0.5, p=5, p=10
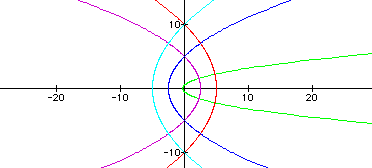
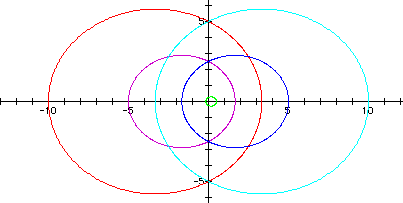
See r=p(0.5)/[1+0.5cos(theta)]
When the trigonometric function is changed from cosine to sine, something somewhat predictable occurs. It appears as if the x and y axes are interchanged. A reflection about the line y=x or, in polar terms, theta = pi/4 and theta = 5pi/4.
k=3 (hyperbola)
k=1 (parabola)
k=0.5 (ellipse)
This coincides with the definitions of cosine and sine. Since cos(theta) = sin(90-theta), and conversely, sin(theta) = cos(90 - theta), the concept of a +90 degree ( +pi/2 radians) rotation can be deduced.
Here are the hyperbolas, with eccentricity 3, just as before but with the 90 degree rotation.
p=-10, p=-5,
p=0.5, p=5,
p=10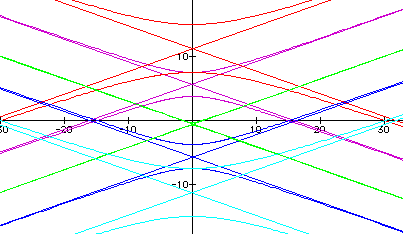
A sum in the denominator will again make a reflection, but this time about the x-axis, or theta = 0 and theta = pi radians (180 degrees). The same patterns follow for the other two conics. For all these conics, the focus is at the origin (0,0). The directrix is changed by the value of p, therefore changing the curvature and/or direction of the conic. Since the distance from the directrix is determined by kr, the smaller k is, the smaller the conic is. When k<1, the conic formed is an ellipse, which contains the least amount of points out of the three formations; k>1 yeilds the conics that contains the most amount of points--the hyperbola.