Just like the spreadsheet can be used to form graphs in the x-y plane with the "scatter" function, polar graphs can be devoloped using the "radar" type graph. The exploration begins with
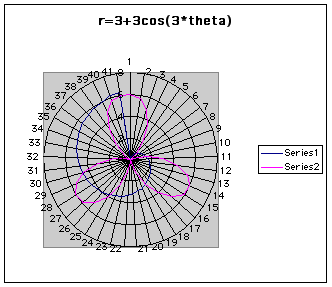
where k is an integer. In the following image, a = b = k = 3. The first column of the spreadsheet is theta in the interval [0, 2pi]. Theta is incremented by 0.05 pi, so there is a total of forty-one points graphed.

Notice the flower, or "rose," has 3 "leaves". Is this because of a, b, or k? Altering the values in the spreadsheet using the formula bar, k is actually the number of "leaves." The following image has k=10.
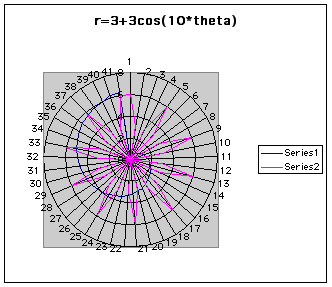
In both of the previous images, the rose has a radius of 3. So the value of k does not affect the girth of the graph. Changing a= b= 5 extends the radius to 5 units. Ultimately, does a or b affect the radius or both?
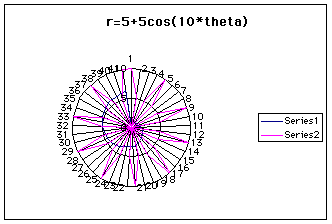
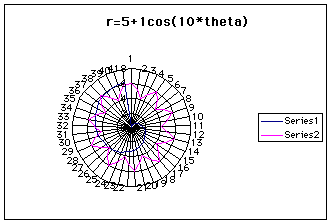
To determine which is the case, I decrease a by 1 several times and examine the graph. Then do the same for b, starting with the original equation, of course. Decreasing a by 1 made the radius of the rose decrease as well, but only by about one-quarter unit each time. Altering b had some interesting results. When b= 4, the radius decreased by half a unit, but then when b=3, the raduis when back to 5 units. The most interesting was when b = 1, which gave the following image.
Changing the signs of a and b only rotates the graph. If k is negative, the graph remains the same since cos(-x) = cos(x). Consider when the a value is taken away, that is a=0 and only
remains. The value of b alters the radius, but not by a whole unit. Increasing b by 1 increases the radius by approximately one quarter unit.
What about the sine function? Does it have the same type rose?
Replacing the cosine and sine function does not yeild much of a difference. Looking at the three-leaved rose, there is an obvious rotation and the removal of a seems to have made the center of the flower "disappear."
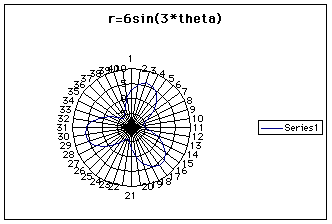
Since sine and cosine are cyclic functions, however, ulitimately the rose would be the same for r=a+bcos(k*theta) as for r=a+bsin(k*theta). Only a rotation of pi/2 radians or 90 degrees would be evident since sin ( theta +pi/2) =cos (theta).