The Circumcenter
by Hilary S. Bell
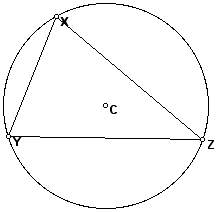
Given any triangle XYZ, the circumcenter C of the triangle is a point equidistant from all three vertices. If a circle is constructed with center C and a radius equal to distance CX (or CY, or CZ), all points X, Y, and Z would lie on the circle.

Given: triangle XYZ
Prove: The perpendicular bisectors are concurrent at point C, the circumcenter.
Let point R be the midpoint of segment XZ, and point S be the midpoint of segment XY. Consider the perpendicular bisectors of segments XZ and XY (shown in the following image in red).

Let the point where the perpendicular bisectors interesect be called point C. Consider triangle XRC and triangle ZRC. They share side RC; both angle ZRC and angle XRC are right angles, so they are conguent, and since line RC is a bisector, segment XR is congruent to segment RZ. Therefore, by Side-Angle-Side (SAS), triangles XRC and ZRC are congruent. It follows that segment XC is congruent to segment CZ (shown in blue in the following image).
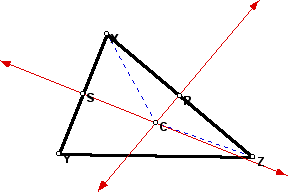
Similarly, since triangle XSC and triangle YSC are congruent by SAS, segment XC is congruent to segment YC.
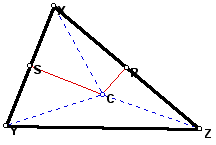
Hence, segments CZ, CX, and CY are all congruent. Now consider triangle CYZ. Since CY and CZ are congruent, it is an isosceles triangle. Look at the angle bisector of angle YCZ (shown in BOLD red in the following image). Let the angle bisector intersect segment YZ at point T.
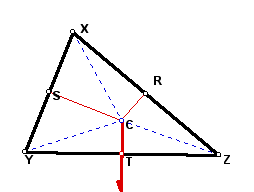
It has been shown that segment CY is congruent to segment CZ. Now, angle YCT is congruent to angle ZCT because of angle bisector CT. Again by Side-Angle-Side, triangle YCT and triangle ZCT are congruent. By the definition of congruent triangles, segment YT is congruent to segment TZ and angle YTC is congruent to angle ZTC ( m <YTC = m < ZTC). By the definition of a straight angle, m < YTC + m < ZTC =180. Using the substitution property, m <YTC + m < YTC = 180 degrees. Solving this, m < YTC = m< ZTC = 90 degrees. Thus, ray CT is the perpendicular bisector of segment YZ.
This proof can also be done on a coordinate plane with vertices of the triangle being (x1,y1),(x2,y2), (x3,y3). The midpoint of each segment can be found using the midpoint formula. The equations to the perpendicular lines can be found as well by determining the negative reciprocal of the slopes between any two of the vertices. Then each set of systems and show they have the same solution. This proof was fun (and long)to work out, but I decided would NOT be fun to type on the computer.