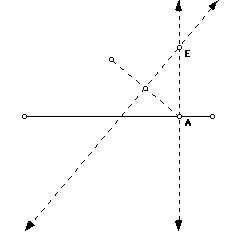
Given a fixed point F as a focus and a line or line segment as a directrix, a parabola can be formed.
1) First an arbitrary point A is chosen on the directrix.
2) A perpendicular line is constructed through the arbitrary point.
3) A segment is made connecting the arbitrary point and the focus, call it segment AF.
4) The midpoint and a perpendicular bisector is constructed on segment AF.
5) The point of intersection of the perpendicular line through point A and the perpendicular bisector of point F will form the parabola.
Click HERE for a script in which moving the arbitrary point A will trace the point that forms the parabola. Like the diagram below.

Here is a diagram with an action button that animates the parabola very nicely. Double click on the animation button to get it started.
Using the locus command, all the points traced are shown. Here is the image with the locus (a parabola) displayed.

The locus of the tangent lines is actually the collection of the perpendicular bisectors of segment AF from the construction. It looks something like this

Here is a sketch with an animation button to see how it is formed. Try shifting the focus F to see the different loci of lines for different parabolas.