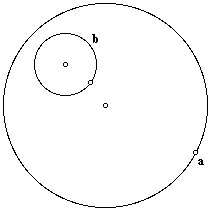
This investigation begins with two given circles a and b, then uses them to construct a third circle c.
The exploration begins with circle a surrounding circle b, like so.

Using the script, the tangent circle c (highlighted in red) is found.
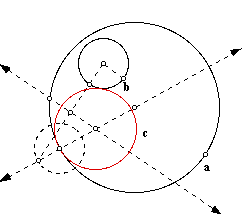
The animation of the point of tangency between circle a and c, and a trace of circle c's center yeilds a locus of point that create an ellipse with the foci being the centers of the two original circles.
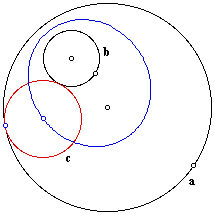
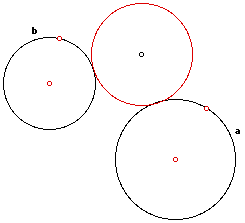
Using the same script, but starting with circle b external to circle a, will also give us a tangent circle c--seen in the red.
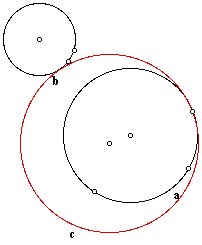
Only this time when we trace the same point as before, instead of an ellipse, a hyperbola is formed. By observing the envelope of circle c's diameters, the outline of the hyperbola is clearly defined. Notice, the foci are still the centers of a and b.

Another method can be used to find the tangent circle when circle a is external to circle b. This method begins with two circles and the tangent is found by using a perpendicular bisector as well. This time, however, the tangent circles that exist between circles a and b are also shown. Click here for a script.
Here is the image of the tangent circle in between.....
The when centers of the tangent circles are traced the points yeild what looks like a very wide hyperbola. Here is an image of the locus of the diameters (also the perpendicular bisectors through the center of the tangen circle). Again the centers of the original circles are the foci of the hyperbola.

If this pattern holds (where the centers are foci for the conic), the conic formed will never be a parabola since a parabola has only one focus. The fourth conic (a circle) can be formed, however, if circles a and b are concentric.