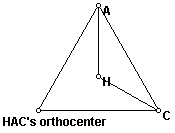
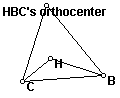
Begin with an acute triangle ABC and find its orthocenter. I use the orthocenter script (repeatedly) from assignment 5. As I find the orthocenters to triangles HBC, HAB, and HAC, I notice these are obtuse triangles. Therefore, their orthocenters are outside of their boundaries--namely on the third vertex: HBC's orthocenter is on vertex A, HAB's orthocenter is on vertex C, and HAC's orthocenter is on vertex B. This is shown by the following examples. (I use different triangles for each example to show that the selection of points A, B, C is arbitrary.)


Here is the image after constructing the circumcircle for all four triangles.
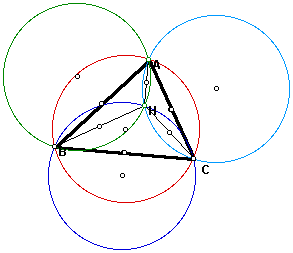
If any one of the vertices A, B or C is moved so that it is concurrent with the orthocenter, two of the circumcircles also become concurrent. If vertex A is moved to H, the circumcircles of ABC and HBC become concurrent. In fact, like the pattern in the previous example, circumcircle of ABC becomes concurrent with HAB if vertex C is moved, and with HAC if vertex B is moved. Showing again that the point chosen is arbitrary.
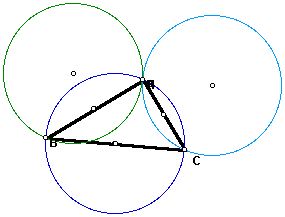
In the particular example above, H is moved to be concurrent with vertex A. H is then located on the circumcircle of ABC and is concurrent with the orthocenter of HBC. When any vertex is moved to become concurrent with the orthocenter, the acute triangle transforms to a right triangle and the opposite side becomes the diameter of circumcircle ABC. For example, when A is moved to be concurrent with H, side BC becomes the diameter of circumcircle ABC.
When the lengths of the radii of the circumcircle are compared, they appear to always be equal.
The link to return is here.