Pedal Triangles
By Hilary S. Bell
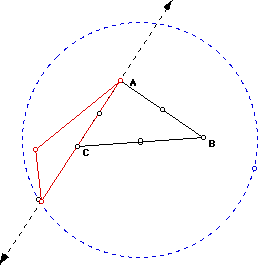
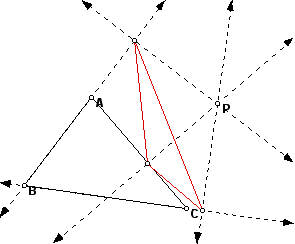
Given any triangle ABC, the pedal point P is chosen to be an arbitrary point in the same plane. Three lines are then constructed passing through the pedal point. Each line is perpendicular to one side of triangle ABC. The pedal triangle then has vertices which are the intersections of the sides of ABC with their corresponding perpendiculars. In some cases, the sides of ABC must be extended to find the point of intersection. In the following image, sides AB and BC were extended as lines to form the pedal triangle. Click HERE for a GSP Script of the pedal point.

The point at which the pedal triangle degenerates into a line is known as the Simson Line. To see an example (yes, there is more than 1!), click HERE.
While exploring the different pedal points and Simson Lines, the hypothesis came that the circumcircle had something to do with the Simson Line. Choosing the pedal point P as an arbitrary point on the circumcircle led to the following locus of Simson Lines.
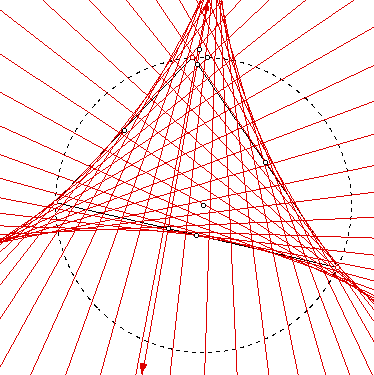
This makes sense since the circumcenter lies on the PERPENDICULAR bisectors of any given triangle, and the pedal point is on perpendiculars to each side of the triangle. For a script that generates the image you see above (given only three points!!), click HERE.
Maybe the Simson Lines are generated on the circumference of any circle centered on the circumcenter? Let's see......
When the circle has a larger radius than that of the circumcircle, no Simson lines are apparent. The pedal triangle is always in three separate segments. For a sketch to manipulate, click HERE.
When the circle has a smaller radius than that of the circumcircle, two vertices of the pedal triangle remain on the sides of the original triangle at all times. As the radius gets larger, only one vertex, and then eventually all vertices are separated from segments AB, BC, and AC.
A side of the pedal triangle in the following image. This is due to the pedal point chosen to be on an extended side of triangle ABC. A vertex of the pedal triangle is also concurrent with the pedal point.