EExtensions
One possible extension of the problem
would be to investigate what happens to the standard sine graph
if you add a constant d to the sine function.
Vary d as you nvestigate graphs of the
form:
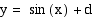
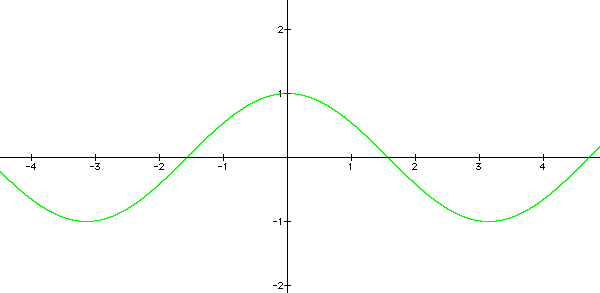
The constant d translates the sine graph
along the y-axis. If d is positive, the graph shifts up the y-axis
by d units. If d is negative, the graph translates down the y-axis
by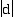 
.
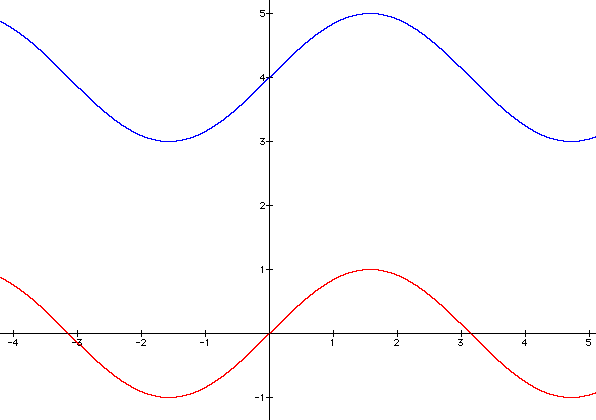
Below is an example to illustrate this
movement of the sine graph. The standard sine graph y = sin x is shown
in red and the graph of y = sin (x)
+4 is shown in blue. Watch
an animation of the graph of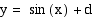
as d varies between -10 and 10.
Another extension is to investigate
similar properties with the graph of y = cos x. What happens to
the graph of:
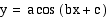as the
values of a, b, and c change?
Below is the graph of the standard equation
of y = cos x. Explore and make comparisons on your own as you
vary a, b, and c. How do the changes with the cosine graphs relate
to the changes with the sine graphs?
