Parametric Curves
by
Summer D. Brown
Investigate each of the following for
0 < t < 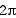 :
:
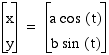
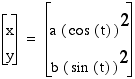
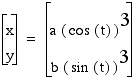
etc.
Describe each when a = b, a < b,
and a > b.
Let's start by exploring 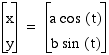 .
.
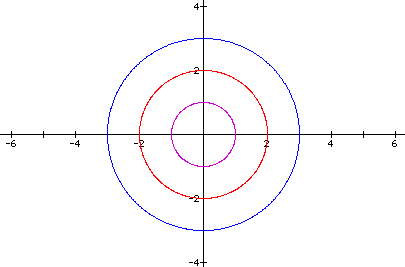
If a =
b, the graph is a circle as shown
in the examples below for a = b = 1, 2, 3. The radius of the circle is equal to 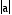 .
.
If a <
b, the graph is typically an ellipse
where the major axis is along the y-axis at a distance of 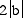 and the minor axis is along the x-axis at
a distance of
and the minor axis is along the x-axis at
a distance of 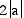 . In the examples
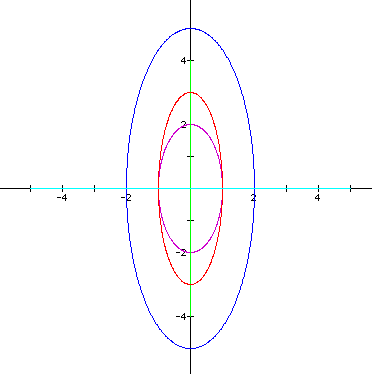
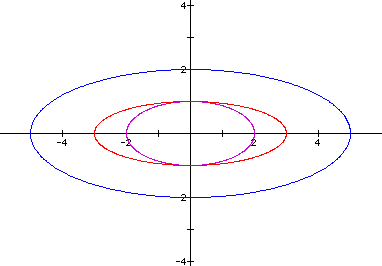
displayed below, (a,b) = (1,2) ; (1,3) ; (2,5) ; (0,4) ; and (-5,0). For (a,b) = (1,2) notice that the graph is
an ellipse where the major axis is along the y-axis and has a
length of 4. The minor axis lies along the x-axis and has a length
of 2.
. In the examples
displayed below, (a,b) = (1,2) ; (1,3) ; (2,5) ; (0,4) ; and (-5,0). For (a,b) = (1,2) notice that the graph is
an ellipse where the major axis is along the y-axis and has a
length of 4. The minor axis lies along the x-axis and has a length
of 2.
When a or b is negative, the graph
is the same as its positive counterpart. In other words, 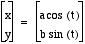 and
and 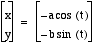 will have the
same graph. (As well as
will have the
same graph. (As well as 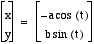 and
and 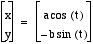 .)
.)
Notice that when a or b = 0, the graph
collapses into a degenerate ellipse, i.e., a line. I have shown
two examples of this in the graph above.
If a >
b, the graph is typically an ellipse.
However in these cases, the major axis will lie along the x-axis
with a length of 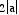 , while the minor
axis will lie along the y-axis with a length of
, while the minor
axis will lie along the y-axis with a length of 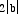 .
See the graphs below for examples where (a,b) = (2,1) ; (3,1); and (5,2). For (a,b)
= (3,1)
, the major axis is along the x-axis and has a length of 6 and
the minor axis lies along the y-axis with a length of 2.
.
See the graphs below for examples where (a,b) = (2,1) ; (3,1); and (5,2). For (a,b)
= (3,1)
, the major axis is along the x-axis and has a length of 6 and
the minor axis lies along the y-axis with a length of 2.
Next, let's explore 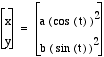 .
.
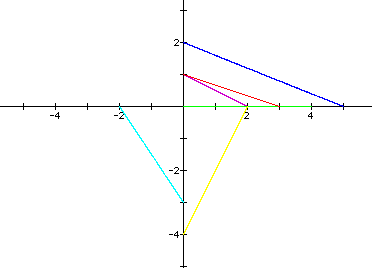
If a =
b, the graph of the parametric equations
is a line that extends from (0,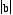 ) to
) to
(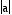 ,0).
Here a and b are the same. Look at the examples below when a
= b = 1,
2,
3.
Once again, the negatives of each of these values will produce
the same graph as their respective positive counterparts. That
is why I specified the absolute value bars in describing the
graphs. The slope of the line segment is the same for each graph.
The slope is equal to -1.
,0).
Here a and b are the same. Look at the examples below when a
= b = 1,
2,
3.
Once again, the negatives of each of these values will produce
the same graph as their respective positive counterparts. That
is why I specified the absolute value bars in describing the
graphs. The slope of the line segment is the same for each graph.
The slope is equal to -1.
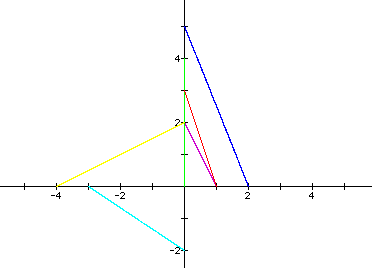
If a <
b, the graph is still a line segment.
In this case, the line extends from (a,0) to (0,b). Take a look
at the examples below where (a,b) = (1,2) ; (0,4) ; (1,3) ; (2,5) ; (-3,-2) ; and (-4,2). Notice that in each case, a < b. Negative
values do make a difference in the graphs, in this case. Here,
the slope of each graph is different. The slope is determined
by the values of a and b, and is equal to -b/a.
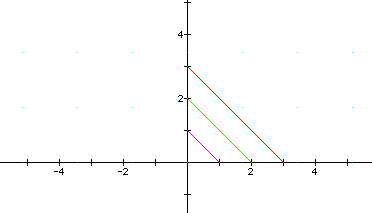
If a >
b, the graph produced is a line
segment which extends from (a,0) to (0,b). The examples below
illustrate the cases where (a,b) = (2,1) ; (4,0) ; (3,1) ; (5,2) ; (-2,-3) ; and (2,-4). The slope of each graph is equal to -b/a.
Next, let's explore the graphs of 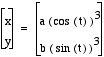 .
.
If a =
b, the graph looks like a diamond
with curved sides. The length of all four arcs that constitute
the sides of the diamond are equal. The graph using the values
(-a,-b) produces the same graph as (a,b). The examples below
display the cases where (a,b) = (1,1) ; (2,2) ; and (3,3). The graph produces four arcs, each connecting
at (a,0) ; (0,b) ; (-a,0) ; and (0,-b). Here, since a and b are
equal, all four arc lengths are equal. The line segment connecting
opposite vertices of the diamond can be called an axis. Each
diamond has two axes, one of which lies along the x-axis and
the other along the y-axis, in these examples. In this case,
both axes are of the same length, because a = b.
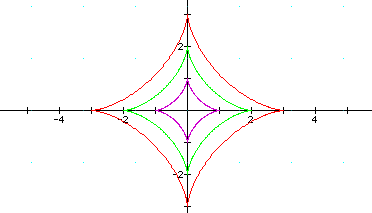
If a <
b, the graph looks like a diamond
with curved sides. Here, the lengths of axes are not equal. The
axis that lies along the y-axis is longer than the axis lying
along the x-axis. We can call the longer axis the major axis
of the diamond. Thus, in this case, the major axis will lie along
the y-axis at a distance of 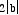 , and
extends from (0,b) to (0,-b). The minor axis will lie along the
x-axis at a distance of
, and
extends from (0,b) to (0,-b). The minor axis will lie along the
x-axis at a distance of 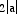 , and extend from
(a,0) to (-a,0). The examples below illustrate the cases when
(a,b) = (1,2)
; (0,4)
; (1,3)
; (2,5)
; (-3,-2)
; and (-2,5).
Notice that you cannot see the graph when (a,b) = (-2,5), because
it produces the exact same graph as when (a,b) = (2,5) in blue.
, and extend from
(a,0) to (-a,0). The examples below illustrate the cases when
(a,b) = (1,2)
; (0,4)
; (1,3)
; (2,5)
; (-3,-2)
; and (-2,5).
Notice that you cannot see the graph when (a,b) = (-2,5), because
it produces the exact same graph as when (a,b) = (2,5) in blue.
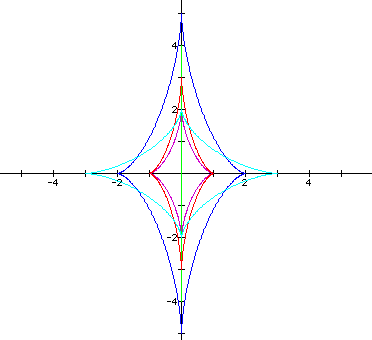
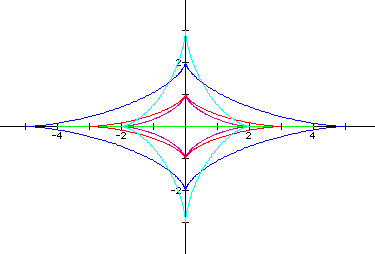
If a >
b, the graph again looks like a
diamond with curved sides. Now, the major axis lies along the
x-axis with a length of 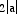 , and extending
from (a,0) to (-a,0). On the other hand, the minor axis lies
along the y-axis with a length of
, and extending
from (a,0) to (-a,0). On the other hand, the minor axis lies
along the y-axis with a length of 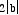 . The
examples below show where (a,b) = (2,1) ; (4,0) ; (3,1) ; (5,2) ; (-2,-3) ; and (5,-2). Again, the graph where (a,b) = (5, -2) is masked
by the graph of (5,2) because they produce the exact same graph.
. The
examples below show where (a,b) = (2,1) ; (4,0) ; (3,1) ; (5,2) ; (-2,-3) ; and (5,-2). Again, the graph where (a,b) = (5, -2) is masked
by the graph of (5,2) because they produce the exact same graph.
We can quickly look at examples of
graphs of 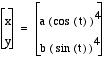 .
.
Below are illustrated the graphs of
the above parametric equation when (a,b) = (1,1) ; (1,3) ; (3,1) ; (-1,3) ; and (-1,-3). The graphs are arcs in one quadrant. Positive
and negative values make a difference in the graphs (consider
(1,3)
and (-1,-3).)
The arcs extend from (a,0) to (0,b).
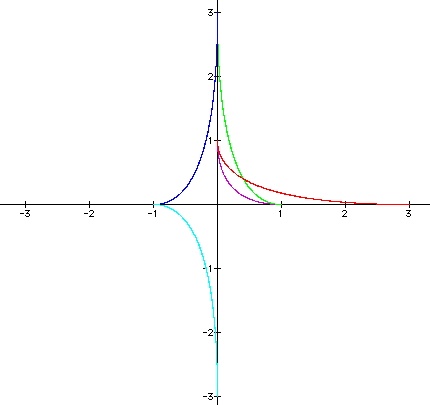
Thus far, the parametric equations with
odd exponents (1,3, etc.) produce a graph that covers all four
quadrants. Also, the negative values of a and b produce the same
graphs as the respective positive values. On the other hand, the
parametric equations with even exponents (2,4, etc.) produce a
graph in only one quadrant. A negative value for a or b produces
a different graph than its positive counterpart. For all parametric
equations of this type, the coordinate points (a,0) and (0,b)
are points on the graph.
With this conjecture, we can predict
that the graph of a fifth degree parametric equation will cover
all four quadrants and that negative values of a and/or b will
produce the same graph as the positive values.
We can test a few examples to see if
they are in line with our conjecture. Graph:
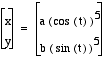 for
(a,b) = (1,1)
; (1,2)
; (2,1)
; (-2,-1)
; (-2,1).
Note that the last two are hidden because they produce the same
graph as (2,1).
for
(a,b) = (1,1)
; (1,2)
; (2,1)
; (-2,-1)
; (-2,1).
Note that the last two are hidden because they produce the same
graph as (2,1).
These examples continue to support our
conjecture. We can further elaborate on our conjecture by stating
that equations with odd exponents plot the points (a,0) ; (-a,0)
; (0,b) ; and (0,-b) as points of the graph. Continuous lines
or curves connect these points. There must be four connecting
curves, each one lying in one of the four quadrants. However,
those with even exponents plot only (a,0) and (0,b) on the x-
and y-axes. Thus, when connecting these points, the graph lies
in only one quadrant.
The conjecture canbe justified with
the following reasoning. We are examining the parametric graphs
when 0 < t < 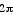 . The
cos (t) and the sin (t) produce positive or negative values depending
on the value of t. Consider the table below:
. The
cos (t) and the sin (t) produce positive or negative values depending
on the value of t. Consider the table below:
| Range of t |
cos(t) |
sin (t) |
Quadrant |
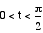 |
+ |
+ |
First |
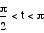 |
- |
+ |
Second |
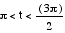 |
- |
- |
Third |
 |
+ |
- |
Fourth |
This will hold true for all odd powers
of n in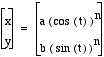 . Thus, the graph covers all four
quadrants. The values of
. Thus, the graph covers all four
quadrants. The values of 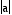 and
and 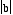 determine the distance the graph extends along the x- and y- axis,
respectively. (a,0) ; (-a,0) ; (0,b) ; and (0,-b) are all points
of the graph since cos 0 = 1, cos
determine the distance the graph extends along the x- and y- axis,
respectively. (a,0) ; (-a,0) ; (0,b) ; and (0,-b) are all points
of the graph since cos 0 = 1, cos  = -1,
sin
= -1,
sin 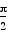 = 1, and sin
= 1, and sin 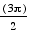 = -1.
= -1.
However for even powers of n, the values
of cos (t) and sin (t) are all positive. Thus, the graph will
only be in the first quadrant. Now, if we add positive and negative
values of a and b, the graph may move to a different quadrant.
But the graph will always be located in only one quadrant. See
the table below (Q stands for the quadrant number):
| |
(a,b) |
(-a,b) |
(a,-b) |
(-a,-b) |
| cos (t) |
Q1 |
Q2 |
Q3 |
Q4 |
| sin (t) |
Q1 |
Q2 |
Q3 |
Q4 |
Since 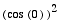 =
= 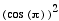 = 1 and
= 1 and 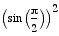 =
= 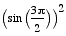 = 1, the only points that lie on the x- and
y-axes are (a,0) and (0,b) where a and b are any integers. This
will be true for all even powers of the parametric equations investigated
here.
= 1, the only points that lie on the x- and
y-axes are (a,0) and (0,b) where a and b are any integers. This
will be true for all even powers of the parametric equations investigated
here.
Thus, the graph of 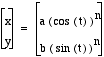 will cover all four quadrants for odd powers of n, but only one
quadrant for even powers of n. The one quadrant for even powers
of n will depend on the sign values of a and b.
will cover all four quadrants for odd powers of n, but only one
quadrant for even powers of n. The one quadrant for even powers
of n will depend on the sign values of a and b.
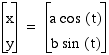
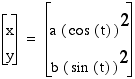
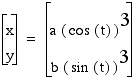
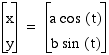 .
..
and the minor axis is along the x-axis at a distance of
. In the examples displayed below, (a,b) = (1,2) ; (1,3) ; (2,5) ; (0,4) ; and (-5,0). For (a,b) = (1,2) notice that the graph is an ellipse where the major axis is along the y-axis and has a length of 4. The minor axis lies along the x-axis and has a length of 2.
and
will have the same graph. (As well as
and
.)
, while the minor axis will lie along the y-axis with a length of
. See the graphs below for examples where (a,b) = (2,1) ; (3,1); and (5,2). For (a,b) = (3,1) , the major axis is along the x-axis and has a length of 6 and the minor axis lies along the y-axis with a length of 2.
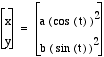 .
.) to
,0). Here a and b are the same. Look at the examples below when a = b = 1, 2, 3. Once again, the negatives of each of these values will produce the same graph as their respective positive counterparts. That is why I specified the absolute value bars in describing the graphs. The slope of the line segment is the same for each graph. The slope is equal to -1.
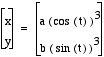 .
., and extends from (0,b) to (0,-b). The minor axis will lie along the x-axis at a distance of
, and extend from (a,0) to (-a,0). The examples below illustrate the cases when (a,b) = (1,2) ; (0,4) ; (1,3) ; (2,5) ; (-3,-2) ; and (-2,5). Notice that you cannot see the graph when (a,b) = (-2,5), because it produces the exact same graph as when (a,b) = (2,5) in blue.
, and extending from (a,0) to (-a,0). On the other hand, the minor axis lies along the y-axis with a length of
. The examples below show where (a,b) = (2,1) ; (4,0) ; (3,1) ; (5,2) ; (-2,-3) ; and (5,-2). Again, the graph where (a,b) = (5, -2) is masked by the graph of (5,2) because they produce the exact same graph.
.
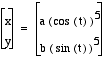 for
(a,b) = (1,1)
; (1,2)
; (2,1)
; (-2,-1)
; (-2,1).
Note that the last two are hidden because they produce the same
graph as (2,1).
for
(a,b) = (1,1)
; (1,2)
; (2,1)
; (-2,-1)
; (-2,1).
Note that the last two are hidden because they produce the same
graph as (2,1).
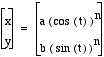 . Thus, the graph covers all four
quadrants. The values of
. Thus, the graph covers all four
quadrants. The values of 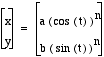 will cover all four quadrants for odd powers of n, but only one
quadrant for even powers of n. The one quadrant for even powers
of n will depend on the sign values of a and b.
will cover all four quadrants for odd powers of n, but only one
quadrant for even powers of n. The one quadrant for even powers
of n will depend on the sign values of a and b.