Pedal Triangles
By: Summer Brown
What is a pedal triangle?
Let triangle ABC be any triangle. Let
point P be any point in the plane. Construct the perpendiculars
to the sides of triangle ABC through point P. The intersections
of the perpendiculars with the sides of triangle ABC form three
vertices of a new triangle, called the Pedal Triangle for Pedal
Point P.
In the example below, the pedal triangle
for triangle ABC with peal point P is shown in pink.
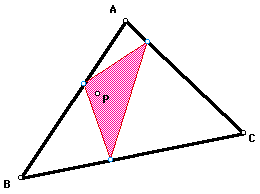
In this investigation, I will explore
what happens to the pedal triangle if the pedal point P is the
centroid, incenter, orthocenter, or circumcenter of triangle ABC.
Some questions worth investigating are:
1. When does the pedal triangle remain
inside the original triangle?
2. What is the relation between the
original triangle and the pedal triangle?
Centroid
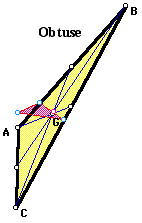
Let the pedal point P be the centroid
of triangle ABC. In these pictures, the original triangle is in
yellow and the pedal triangle in pink.
The pedal triangle seems to remain inside
triangle ABC when triangle ABC is acute or right. When triangle
ABC is obtuse, the pedal triangle does one of two things: it remains
completely inside triangle ABC, or one vertex reaches slightly
outside of the original triangle.
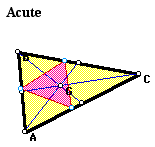
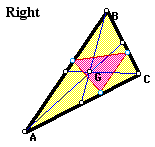
I did not find any relation between
the original triangle and the pedal triangle.
Incenter
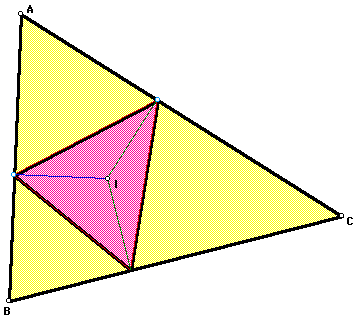
Let point P be the incenter of triangle
ABC.
In all cases, whether triangle ABC is
acute, right, or obtuse, the pedal triangles always remains inside
the triangle.
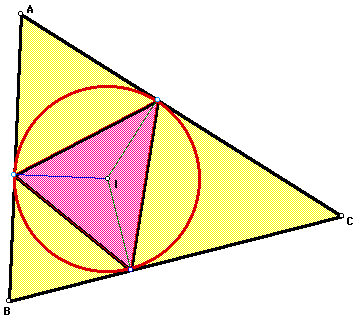
One observation to make is that the
incircle of triangle ABC is the circumcircle of the pedal triangle.
This is because the pedal point is the incenter. To find the vertices
of the pedal triangle, you must construct the perpendiculars from
the pedal point to each side of triangle ABC. The segment formed
from the pedal point to the foot of the perpendicular are radii
of both the incircle of triangle ABC and the circumcircle of the
pedal triangle. Thus, since the circles have the same center and
radii, they are concurrent.
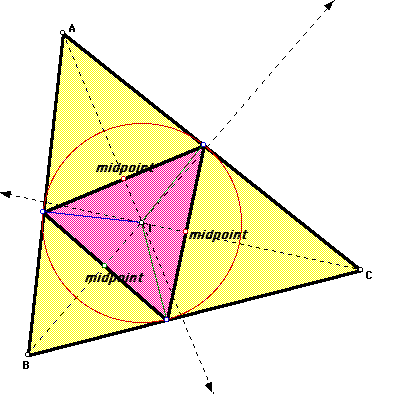
Another observation is made when the
angle bisectors (dashed lines) of triangle ABC are drawn in. The
angle bisectors intersect each side of the pedal triangle at each
respective midpoint. Click
here to see a proof and explore with the GSP sketch.
Orthocenter
Let point P be the orthocenter H of
triangle ABC.
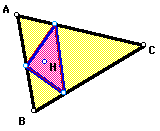
In all cases, the pedal triangle is
equal to the orthic triangle of triangle ABC.
If triangle ABC is acute, then the pedal
triangle remains inside triangle ABC.
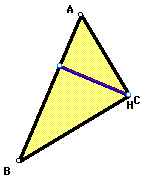
If triangle ABC is right, then the pedal
triangle is a straight line, or a degenerate triangle. The pedal
point H lies on the vertex of the right angle.
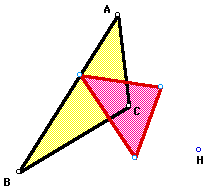
If triangle ABC is obtuse, then the
pedal triangle moves outside of triangle ABC. Also, the pedal
point no longer remains inside triangle ABC. As the obtuse angle
becomes greater, the pedal point moves farther and farther away
from triangle ABC.
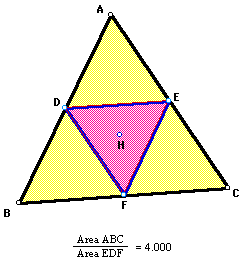
Another interesting observation is that
when triangle ABC is equilateral, the pedal triangle also becomes
equilateral. In fact, the pedal triangle will always have an area
one-fourth the size of triangle ABC when it is equilateral. Click here for a proof of this observation.
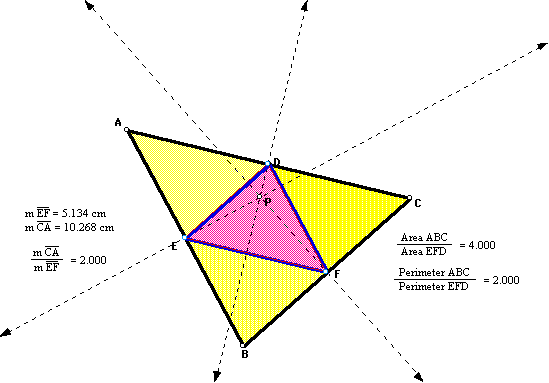
Circumcenter
Let point P be the circumcenter of triangle
ABC.
The pedal triangle will always remain
inside triangle ABC, even if P moves outside of triangle ABC.
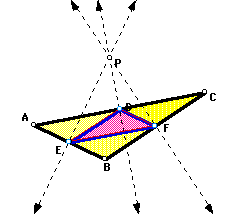
The pedal triangle is equal to the medial
triangle of triangle ABC.
In all cases, the ratio of the area
of triangle ABC to the pedal triangle is 4 to 1. Also, the ratio
of the respective perimeters is 2 to 1.
Triangle ABC is divided into 4 congruent
triangles, with the pedal triangle being one of these. Thus, the
pedal triangle makes up one-fourth of the area of triangle ABC.
The pedal triangle is similar to triangle
ABC with sides having lengths 1/2 the lengths of triangle ABC.
Click here to explore with a GSP sketch.