Explorations of
Linear Functions
Assignment #1 EMAT
6680
By
Mary Bruce
Looking at two linear functions, f(x) and g(x), properties of the following will be examined:
i. h(x) = f(x) + g(x)
ii. h(x) = f(x)·g(x)
iii. h(x)=f(x)/g(x)
iv. h(x)=f(g(x))
Typically, a high school algebra textbook will introduce linear functions and often prompt the students to perform various combinations and compositions of linear functions. Frequently the book emphasizes the algebraic representations of these combinations without reference to the corresponding graphs. Exercises in which students are given two linear functions and asked to find .i-iv above are common. Many students routinely perform the necessary calculations void of an awareness of existing graphical representations or connections.
After studying various algebraic properties it is natural for one to query whether the set of linear functions is “closed” under addition, multiplication, division and in composition. It seems relevant to encourage students to explore the “closure” of linear functions for various operations. In addition, through a graphical exploration, one can discover a synthesis among various types of functions rather than an often fragmented and disconnected understanding that so often occurs.
Starting with two rather simple linear functions we analyze the sum h(x) = f(x) + g(x):
f(x) = 2x + 3
g(x) = 5x + 1
h(x) = (2x + 3) + (5x + 1)
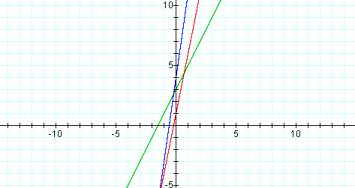
One can easily notice from the graphs that the slope of the sum is steeper than the two originals, and the y-intercept is larger than either of the individual functions. Closer analysis reveals the slope and y-intercepts to be the actual sum of the individual values respectively. This is exactly what one should expect: (ax + b) + (cx + d) = ax + cx + b + d = (a + c)x + (b + d). The student can then process that the sum of two linear functions will also be a linear function with a slope and y-intercept that is the sum of the two individual values respectively. Thus “closure” of linear functions for addition seems to hold.
f(x) = -2x + 3
g(x) = -4
h(x) = (-2x + 3) + (-4)
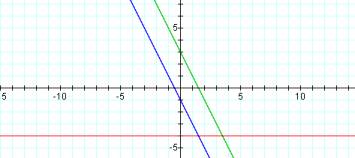
Using a constant function in conjunction with looking at the graph should give a better understanding as to why we would end up with a graph that is parallel but translated 4 units down from the original graph.
f(x) = -2x + 3
g(x) = 2x – 3
h(x) = (-2x + 3) + (2x – 3)
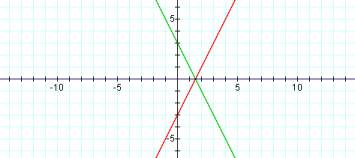
Varying the slopes and y-intercepts and making them opposites, the student can grasp the significance of direction when combining two individual graphs.
Whereas linear functions are “closed” under addition, we would not expect this to be true for multiplication. An algebraic inspection (ax + b)(cx + d) = (ac)x² + (ad + bc)x + (bd) leads us to the conclusion that we would expect a product that is a quadratic function.
f(x) = x – 3
g(x) = x + 5
h(x) = (x – 3)(x + 5)
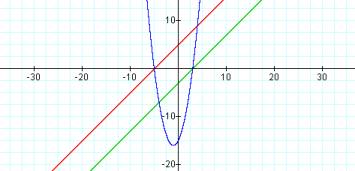
Looking at the graphs of h(x) = f(x)·g(x) the parabola confirms our expectation. One notices from the graph that the x-intercepts (roots) of the quadratic are the same as the x-intercepts of the two original linear functions thus allowing the student to synthesize the concept of a quadratic function as the product of two linear factors. Also from the graph one can easily notice the x-coordinate of the vertex falls exactly halfway in-between the x-intercepts acting as a sort of “balancing point” between the two intercepts.
f(x) = 2x – 1
g(x) = -x + 3
h(x) = (2x – 1)(-x + 3)
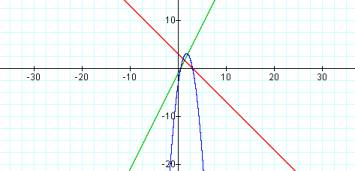
One can conclude from the graph that the product of linear functions with opposite slopes will produce a quadratic function with a negative leading coefficient and thus downward parabolic shape.
One must question whether two linear functions will ALWAYS yield a quadratic function. Careful analysis confirms the negation.
f(x) = 4x – 2
g(x) = 3
h(x) = 3(4x – 2)
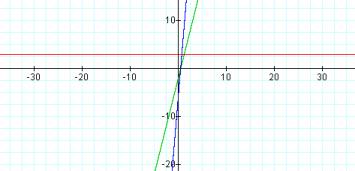
One can make a connection with the roots of a quadratic equation and realize unless it is a double root, a quadratic function cannot have just one real root and thus we see that in this special case the product of two linear functions is NOT always a quadratic function.
Thirdly, we examine the possible “closure” of linear functions with division: h(x) = f(x)/g(x) and in our exploration make a discovery of a connection between linear and rational functions.
f(x) = x – 3
g(x) = x + 2
h(x) = (x – 3)/(x + 2)
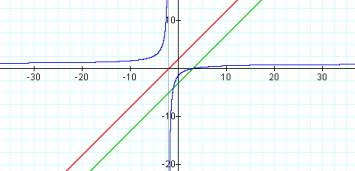
We see that the quotient of two linear functions produces a hyperbola with a vertical asymptote at the same place as the x-intercept of g(x). This should make sense as the vertical asymptote is always where the denominator equals zero. Secondly we notice the hyperbola has an x-intercept that coincides with the x-intercept of f(x). This enriches our understanding of an x-intercept of a rational function as a value where the numerator equals zero.
f(x) = x – 3
g(x) = 2x – 6
h(x) = (x – 3)/(2x – 6)
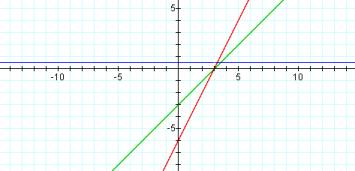
One can verify that the quotient of two linear functions will NOT always result in a rational function thus giving credibility to h(x) = (x – 3)/(2x – 6) = (x – 3)/2(x – 3) = ½ which is a horizontal line through y = ½.
Finally we examine the composition of two linear functions h(x) = f(g(x)). We speculate a(cx + d) + b = (ac)x + (ad + b) that we will most likely get another linear function.
f(x) = 2x – 3
g(x) = x + 6
h(x) = 2(x + 6) – 3
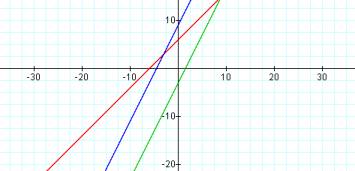
f(x) = 2x + 3
g(x) = (x -3)/2
h(x) = 2((x -3)/2) + 3
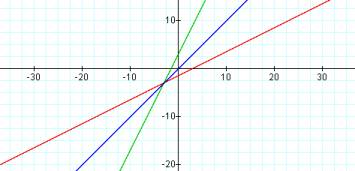
We can verify from the graph that the composition of two linear inverses produces a graph that is the line y = x.