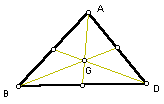
CENTERS OF A TRIANGLE
EMAT 6680 - Assignment 4
by Mary Bruce
When studying triangles in a standard geometry course, students typically study and often construct points of concurrency within a triangle.
The CENTROID(G) is formed at the intersection of the three medians of a triangle:

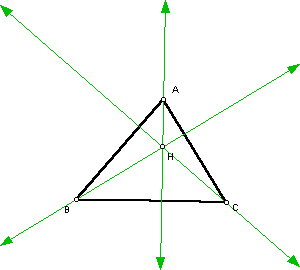
The ORTHOCENTER(H) is formed at the intersection of the three altitudes of a triangle:
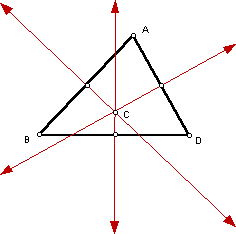
The CIRCUMCENTER(C) is formed at the intersection of the three perpendicular bisectors of a triangle:
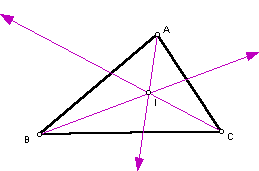
Finally the INCENTER(I) is formed at the intersection of the three angle bisectors of a triangle:
In this writeup the author explores these centers of a triangle not as separate and disjoint points of concurrency but rather as centers often sharing significant mathematical relationships.
Using GSP one can construct a triangle showing all points of concurrency simultaneously and through manipulation of the sketch, relationships are easily noticed. The following construction shows all points with the Euler line (segment joining C, G and H) in red:
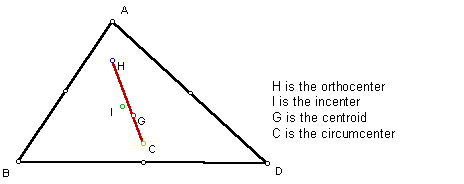
Having learned to classify triangles according to its sides and angles, students can then explore through GSP the behavior of these concurrent points for various types of triangles.
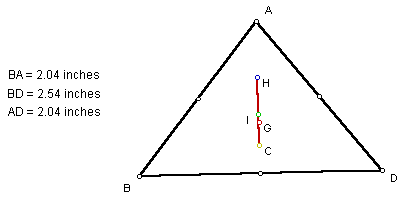
It appears that in an isosceles triangle, all four points are collinear and fall on the Euler line:
In an equilateral triangle all points seem to coincide at the same place:
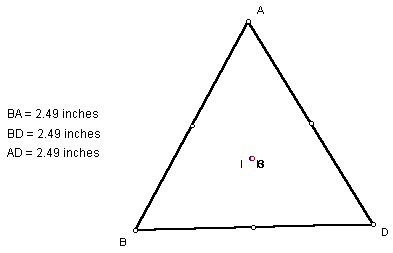
This should follow logically from the discovery that in an equilateral triangle, the medians, angle bisectors, perpendicular bisectors and altitudes are all the same.
Looking at angle classifications, it appears that for an acute triangle all points of concurrency are inside the triangle as shown:
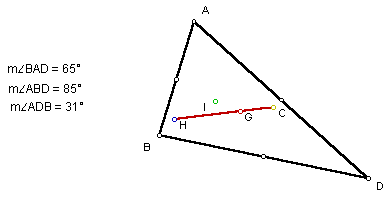
For an obtuse triangle the circumcenter (C) and orthocenter (H) appear to be outside the triangle:
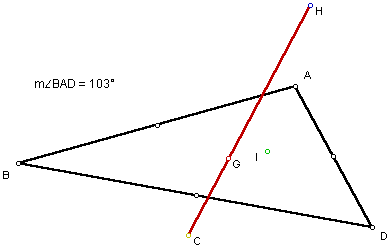
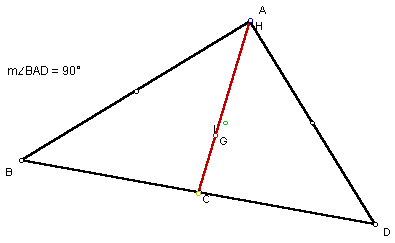
For a right triangle one notices that H lies at the vertex of the right angle and that C lies on the midpoint of the opposite side:
H and C then exit the triangle from this vertex and midpoint as the triangle becomes obtuse and these points move to the outside of the triangle.
The fact that in a right triangle H lies on a vertex and C lies on the midpoint of the opposite side should draw attention to the fact that segment HC would then be considered a median of that right triangle. Thus G should be 2/3 the distance from H to C as the centroid always is. One should then question whether G is ALWAYS 2/3 the distance from H to C on the Euler line regardless of whether it is a right triangle or not.
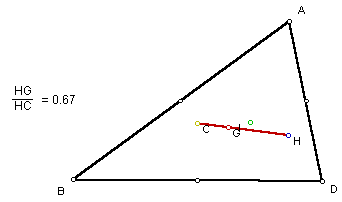
Click here to manipulate a sketch by translating a vertex and analyzing the ratio of HG to HC.