
BEYOND THE AREA OF A TRIANGLE
by Mary H. Bruce - EMAT 6690

This essay was prompted by an inquiry from two of my advanced students regarding a mathematics contest question. It is customary perhaps to first introduce the concept of area of geometric figures as the number of square units that make up the interior of a figure. A rectangle would serve as an easy figure to start with since there would be no partial squares in the interior:
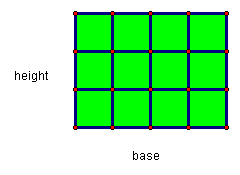
Students are able to count the squares and determine the area to be 12 square units. This introduction also reinforces the reasoning as to why area is measured in square units. Students should be able to recognize that if you take the base and multiply it by the height you will get the area and thus Area = Base · Height. Students should also deduce that area refers to the region inside a figure. Connections can be made to problems such as: If there are 4 rows of desks and each row has 3 desks, how many desks cover the floor? 4 · 3 = 12 in a rectangular array of desks and this can help to solidify the formula for the students.
Next, students could be presented with a parallelogram:
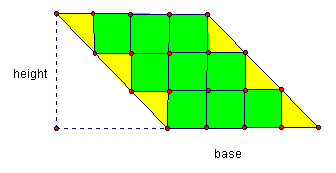
Counting square units one would notice the half-squares in yellow and by combining two half-squares to make a whole, one notices the area of the parallelogram is the same as the previous rectangle. Students could then be asked to cite similarities with the rectangle and intuitively reverting back to the rectangle formula would hopefully lead them to notice the base and height of the parallelogram are the same. This is also a good time to reinforce the concept of the height of a geometric figure as not necessarily being just another side. After making these connections between the area of the rectangle and parallelogram, students should recall that a rectangle is, in fact, a parallelogram and thus should share the same area formula.
Have the students imagine the following figure as a blanket:
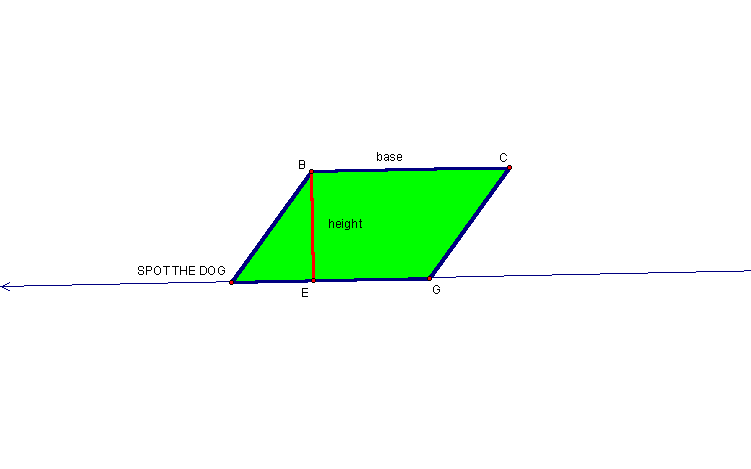
Click here and then click on Animate to simulate Spot the Dog pulling on the blanket. Would the blanket's area change? No, it is the same material that made up the original blanket. Notice the base and height remain constant throughout the simulation and, thus, the area of the quadrilateral remains unchanged.
If opposite vertices of a parallelogram are connected, are the two resulting triangles congruent?
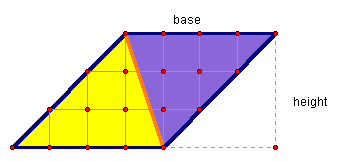
Through either SSS or SAS, one can conclude that they are and since congruent figures have the same area, then each triangle must be one-half the area of the parallelogram. One can easily notice that the resulting triangles have the same base and height as the parallelogram, thus the area of a triangle = 1/2 Base · Height.
Suppose we connect two of the medians of a triangle. Do the shaded regions have the same area?
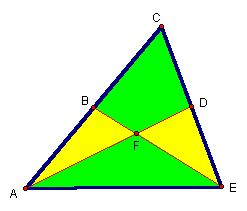
Proof: Draw segment BD. We know then that segment BD || segment AE and is half its length.
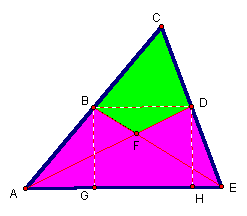
Thus segment BG is congruent to segment DH and the heights of ΔABE and ΔEDA are the same. Both triangles share the same base AE and, thus, by Area = 1/2 B·H, both triangles have equal areas.
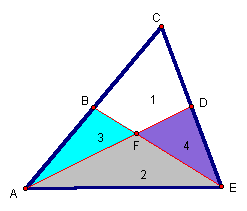
Since ΔABE = region 2 + region 3 and ΔEDA = region 2 + region 4 then through substitution and subtraction properties, the area of region 3 = area of region 4. It is important here to emphasize that this does not necessarily mean the figures are congruent.
It is still necessary to show that the area of region 1 = area of region 2.
Draw a line parallel to segment CE that passes through vertex A.
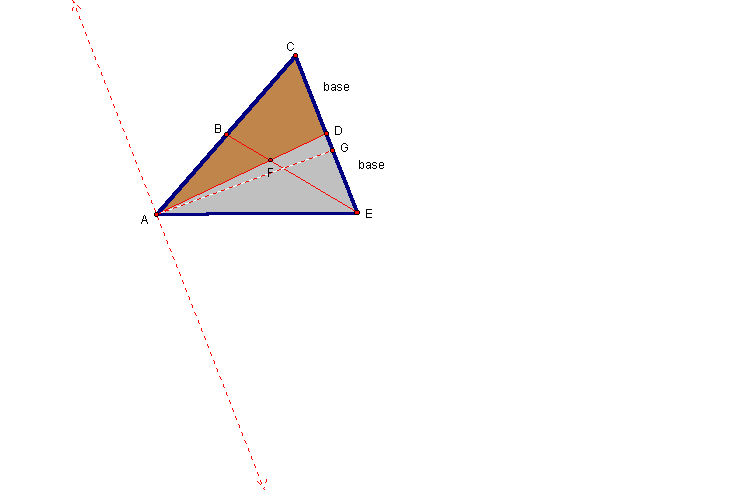
Since segment AD is a median, then base CD is congruent to base ED and both ΔACD and ΔAED have the same height AG. Thus by A=1/2 Bh, both triangles have the same area.
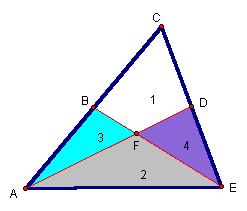
Since area of ΔACD = region 1 + region 3 and area of ΔAED = region 2 + region 4 and since area of region 3 = area of region 4, then by substitution and subtraction properties, we know area of region 1 = area of region 2.
Next, the author looks at an area of a triangle problem in which each side of a triangle has been trisected:
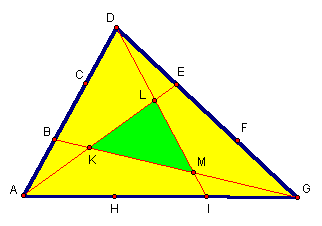
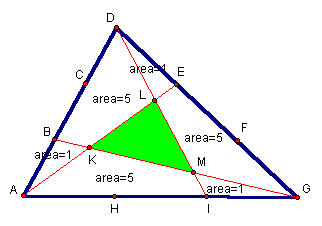
Given the following areas of regions, find the area of the shaded region:
Draw a line parallel to segment DG that passes through vertex A:
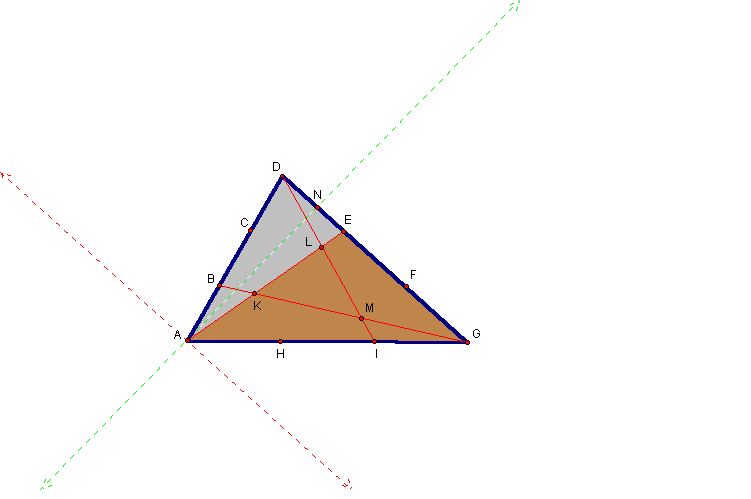
Since ΔADE and ΔAGE both have the same height AN and since base GE is two times base DE then the area of ΔAGE must be twice the area of ΔADE. Noticing the congruent regions,
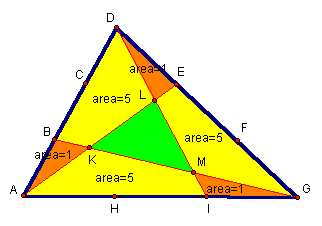
one realizes that the area of ΔADE = 7, thus the area of ΔAGE = 14 which leaves the area of the shaded ΔLKM to equal 14 - 11 = 3. Through GSP technology it can be shown that the ratio of the area of this shaded region to the area of the big triangle will always be 1/7. Click here for a demonstration.
The author still seeks to prove how the small triangles have the same area and how the quadrilaterals have a 5 to 1 area ratio with the small triangles in order to complete a proof of this 1/7 area relationship.
Similarly, the mathematics contest problem:
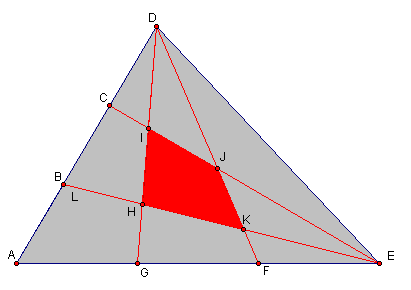
Given that two sides of a triangle are trisected as such and the area of ΔADE = 1, find the area of the shaded region. Through an analysis using GSP, the author realizes the following equality of areas:
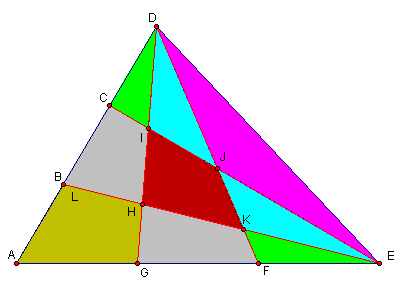
Through GSP, it becomes evident that regardless of the area of ΔADE, the ratio of the area of shaded quadrilateral HIJK to the area of ΔADE will always be 9/70. Click here for a demonstration.
After hours of mental anguish in seeking to arrive at a geometric solution to this problem, the author has decided that just as galaxies in this vast universe, the answer simply lies somewhere out there.
RETURN to Mary's Home Page