A PROBLEM-SOLVING APPROACH TO AREA RATIOS
by Mary H. Bruce - EMAT 6690
In my AP Statistics class this year, I gave a computer-based assignment illustrating simulation to solidify the concepts of sampling distributions of means and proportions. Some of the directions were direct and specific. I asked the students to create normal and skewed populations and then simulate sampling distributions from each for various sample sizes. Subsequently, I asked the students to create their own populations and analyze the results. The students returned the following day dumfounded at this last requirement. "What do you mean by 'Analyze'?" they asked. I personally attribute this confusion to be a by-product of years of mathematical instruction saturated by rote exercises and the lack of student-centered explorations. As the NCTM Standards state, "a major goal of high school mathematics is to equip students with knowledge and tools that enable them to formulate, approach and solve problems beyond those that they have studied." It is necessary to give secondary students explorative exercises that require the students to analyze, explore and investigate.
Consequently, this essay is adapted from the article "Fostering Mathematical Curiosity," Mathematics Teacher Vol. 95, No. 2 February 2002. The author of the article presents an explorative approach to an area problem typical of a high school geometry or algebra II course after the student has been exposed to quadratic functions. In the article, the author focuses on the ratio of areas in an equilateral triangle. In an attempt to provide an extension to the article, this essay will focus primarily on the ratio of areas within a square and hexagon.
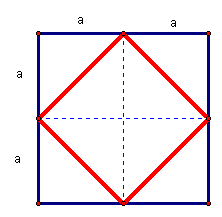
Given a square, construct another square by joining the midpoints of the four sides of the original figure. What is the ratio of the area of the smaller square to the area of the larger square?

Geometrically, it is easy to see that the area of the inner square is 2 square units and the area of the larger square is 4 square units. Thus, the ratio of the areas is 1/2. Algebraically, we could show that the area of the larger square is 2a·2a which is 4a² whereas the sides of the inner square would be a√2 because of the 45˚-45˚-90˚ triangle. The area of the inner square would, therefore, be a√2 · a√2 which gives 2a² and again shows a ratio of areas of 1/2.
Suppose we explore further beyond a square formed at the midpoints of the sides and move the four vertices of the inner square along the sides of the original square. Using GSP we can animate and calculate a continuous side ratio to area ratio and plot the coordinates of each. CLICK here for an illustration.
Notice from the trace of the plotted point that the ratio of the sides to the areas is a quadratic function with a minimum at the previously discussed 1/2 ratio. The simultaneous viewing of the two squares along with the generation of the parabola eases the comprehension of such a relationship.
Suppose we extend the sides of the inner square beyond the sides of the original square. Would the quadratic relationship remain? CLICK here to further the investigation.
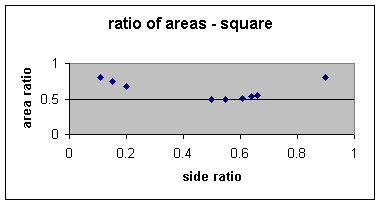
Suppose we wish to determine the quadratic equation that best fits the data. Using Microsoft Excel, we can generate a scatterplot from random coordinates of the side and area ratios.
| side ratio | area ratio |
| 0.2 | 0.68 |
| 0.15 | 0.75 |
| 0.11 | 0.81 |
| 0.5 | 0.5 |
| 0.61 | 0.52 |
| 0.55 | 0.5 |
| 0.64 | 0.54 |
| 0.66 | 0.55 |
| 0.9 | 0.81 |
Fitting a quadratic curve to our data, we can use Excel to generate our best fit equation:
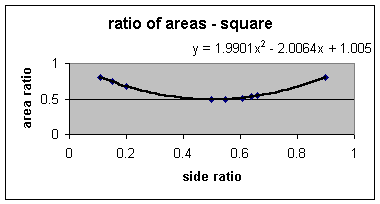
Analytically we arrive at a similar quadratic equation:
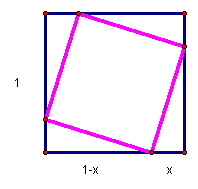
Letting each side of the square be 1 unit and then splitting each side into two parts, x and 1-x, we determine the area of the smaller square to be the larger square minus the 4 triangles which gives 1 - 4(1/2)(x)(1-x) = 1 - 2x + 2x². Thus the ratio of the inner square to the outer is 2x² -2x + 1 to 1 which gives a quadratic equation close to the excel estimation.
The author of the Mathematics Teacher article derived a quadratic equation for the triangle model of 3x² - 3x + 1 and referenced a pentagon to give 1.3x² - 1.3x + 1.
Would a hexagon also produce a quadratic relation? CLICK here to investigate.
It appears that, in general, regardless of the polygon, the ratio of sides and areas will produce a quadratic function. It is evident from the trace of the plotted point that the vertex will always have an x-coordinate of 1/2 though the y-coordinate increases as the sides of the polygon increase. Analytically we can determine that the quadratic equation that fits the hexagon would be x² - x + 1. CLICK here for an explanation.
It is evident from the investigation that the quadratic function that fits these ratios is a function of the form ax² - ax + 1. Students at an algebra II level can understand why the coefficients of the quadratic and linear terms must be the same. The x-coordinate of the vertex of the parabola must occur at a/2a which reduces to 1/2. Students can also make sense out of the constancy of the y-intercept at (0,1) regardless of the polygon. When the ratio of the side lengths is zero, then the two polygons coincide and, thus, results in a 1 to 1 area ratio.
Finally, one should naturally consider a possible relationship between the polygon and the matching coefficients in the resulting quadratic equation. Entering the data in an excel spreadsheet yields the following graph:
| # of sides | coefficient | |
| 3 | 3 | |
| 4 | 2 | |
| 5 | 1.3 | |
| 6 | 1 |
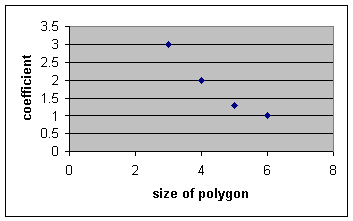
Based on the nature of the data and the resulting graph, we could fit an exponential function to the data to obtain the following:
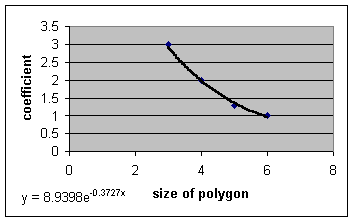
One can conclude from this exponential relation that the coefficients would approach a limit of zero thus resulting in the original quadratic function of the area ratios approaching a limit of 1. Due to the technology, students need not have a background in limits to understand that the more sides a polygon continues to have, the more the area of the inner polygon will come closer and closer to the actual size of the original polygon, thus resulting in side and area ratios with much lower variation and an overall proximity to 1. The inclusion of technology in the comprehension of such an investigation is vital.
RETURN to Mary's Class Page