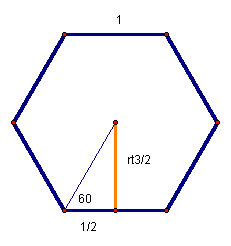
Let one side of a regular hexagon be 1.  Area of a regular polygon = 1/2 Pa where P is the perimeter and a is the length of the apothem.  Thus area of the hexagon = 1/2 (6) (√3/2) = 3√3/2.

Draw a hexagon inside the original hexagon.

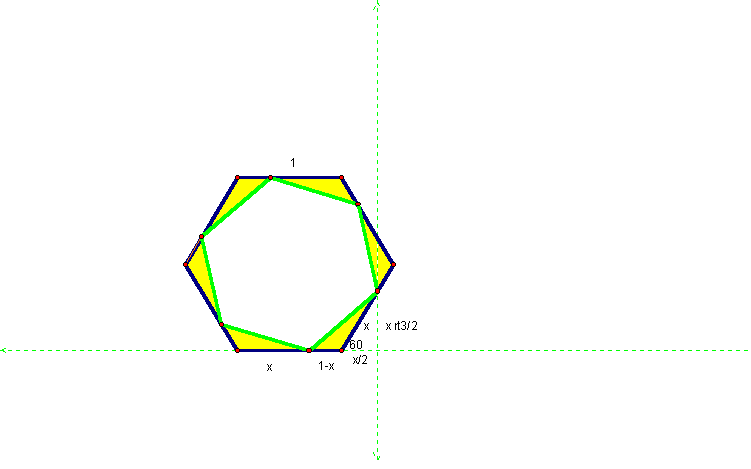
    Extend a perpendicular to create a 30-60-90 triangle.  Thus the area of a yellow triangle is A = 1/2 (1-x)(x√3 /2).  Since there are 6 congruent shaded triangles we multiply by 6 to get 3(1-x)(x√3 /2) = 3/2(x√3 - x²√3).  To get the area of the inner hexagon, we find the difference in the area of the original hexagon and the 6 triangles:  3√3 /2 - 3/2( x√3 - x²√3).  The ratio of the areas is thus (3√3 /2 - (3x√3 /2 - 3x²√3 /2) / (3√3 /2) = (3√3 /2 - 3x√3 /2 + 3x²√3 /2) / (3√3 /2) which simplifies to 1-x + x².

RETURN to essay 2