DAY 4 - Sine and Cosine Graphs - Mary H. Bruce - EMAT 6690

Objective:  Students will be able to graph equations of the form y = a sin x and y = a cos x

From the previously discussed coterminal angles and repetitive values on the unit circle, one can speculate that the trigonometric functions will be periodic and repeat in regular cycles.  Taking the unit circle and plotting radians (x axis) versus the y-coordinate of the (x,y) ordered pairs on the unit circle, one can generate one full cycle or period of the graph y = sin x (remember sin x is the y-coordinate when the radius is 1).  As a point rotates counterclockwise around the unit circle, it is easy to see from a GSP sketch how the trigonometric graphs unfold.  Students should calculate their own table of exact values from the unit circle to correspond with the decimal values from the GSP sketch.  CLICK here for a GSP animation of y = sin x.  One should notice that the sine graph is bounded between -1 and 1 (tie this in to previous discussion), a maximum occurs at Π/2 and a minimum at 3Π/2 with intercepts at 0, Π and 2Π (tie this in to y-coordinates from the unit circle).  Technology helps to reinforce the concepts of amplitude, period, maximum and minimum values and intercepts as related to the unit circle itself.

Students can construct a table of values for the y = cos x graph as well.  Have students guess at the shape, the amplitude, the period, the maximums, the minimums and the intercepts.  CLICK here for a GSP animation of the cosine curve.

Just as students are familiar with graphing from algebra whereby coefficients and constants may affect the graph itself, students should be encouraged to explore with technology the various transformations of trigonometric graphs.

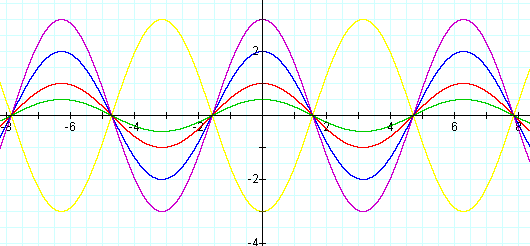
Consider the graph of y = 2 cos x.  Would a coefficient in front affect the period of the parent graph y = cos x? How would a negative coefficient affect the graph? Observe a Nucalc illustration of the graphs of y = cos x,  y = 1/2 cos x,  y = 2 cos x,  y = 3 cos x and y = -3 cos x.

The coefficient in front does not change the argument of the cosine and thus only changes the graph in the vertical direction.  The period (length of one full cycle), intercepts, maximum and minimum domain values are not affected by this number.  The amplitude is magnified according to this value, and a negative value reflects the graph over the x-axis (tie into f(x) and -f(x) from algebra).

Exercises:  Graph the following:  y = 1/3 sin x

                                                    y = 5 cos x

RETURN to Instructional Unit Outline