DAY 5 - More Sine and Cosine Graphs - Mary H. Bruce - EMAT 6690

Objective:  Students will be able to graph trig functions of the form y = a cos bx, y = a sin bx, y = a cos bx + c,  y = a sin bx + c,  y = a cos (bx + d) + c

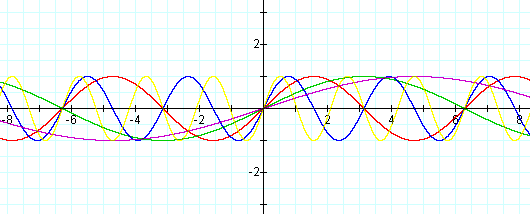
Continuing discussion from day 4, suppose we place the coefficient in front of the argument x.  How would the graph of  y = sin 1/2 x change from the parent graph y = sin x?  Would the amplitude be affected?  From day 4 discussion, one should realize the amplitude will still be 1.  The argument is now multiplied by 1/2 which will take the graph twice as long to complete one revolution thus affecting the period, or length of a full cycle.   Suppose the equation is y = sin 2x.  Compare the graphs of y = sin x,  y = sin 1/2 x,  y = sin 2x,  y = sin 1/3 x,  y = sin 3x.   See if you can discover a mathematical relationship between the "b" in the formula y = sin bx and the period.

It appears that the period = 2Π/b.

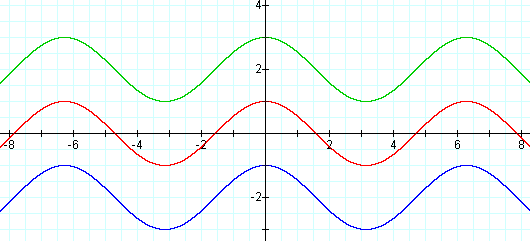
Suppose we add or subtract a constant to the function.  Many of the concepts in trig graphs should be connected to graphing shifts learned in algebra II ( for example f(x) and f(x) + c).  One would guess that we would witness a vertical translation in the same direction as the constant itself.

The graphs of  y = cos x,  y = cos x + 2,  y = cos x -2  follow:

Finally consider the transformation by adding or subtracting a constant inside the function (tie in to f(x) and f(x + c)).  One would guess a horizontal translation of x + c = 0.  Consider the graphs y = sin x,  y = sin(x + 3),  y = sin(x - 3):

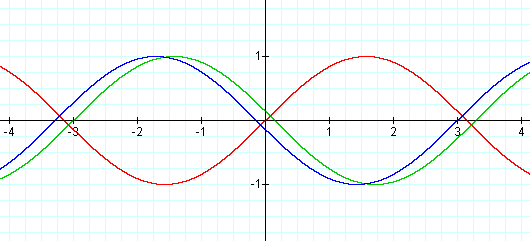
In trigonometry, we call these horizontal shifts phase shifts.

Students should experiment with the technology and combine several types of transformations within one function to detect the changes in the parent graph.

Exercises:  Graph the following:

                        y = sin 1/4 x

                        y = cos (x - Π/4)

                        y = sin (x + Π/2) + 3

                        y = 2 cos 4(x - Π) - 2

RETURN to Instructional Unit Outline