Parametric Curves
EMAT 6680 - Assignment 10
by Mary Bruce
A parametric curve in the plane is a pair of functions
x=f(t)
y=g(t)
where the two continuous functions define ordered pairs (x,y). In this assignment, the author will write parametric equations of a line through (7,5) with a slope of 3.
Exploring sets of curves for x=a + t
and y= b+kt, the author discovered various linear graphs.
Click here to view the NuCalc animation of
the parametric equations
. As the values of k change, one
notices a change in the slope of the line though despite the movement, it is
easy to notice a point that remains stationary throughout. At a closer
glance, one notices this fixed point to be (3,5) from the parametric equations
above. Looking specifically at the parametric equations
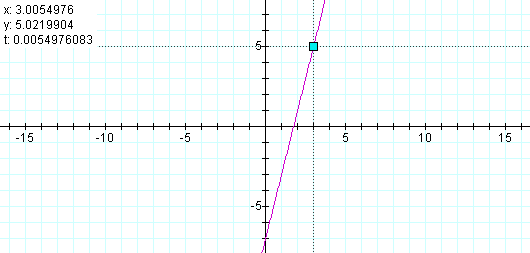
one notices that not only does the point (3,5) fall on the graph at t=0 (approximation) but that the slope of the line appears to be k=4. Based on this assumption, the parametric equations for the line through (7,5) with a slope of 3 should be
Algebraically we know that the equation of this line is y-5=3(x-7) which yields y=3x-16 with slope of 3 and y-intercept of -16. In general, x=a+bt and y=c+dt are the parametric equations of a line (both b and d ≠ 0). Through substitutions we have x=a+bt and then solving for t obtain t=(x-a)/b. Replacing t in the y=c+dt equation, we have y=c+d((x-a)/b) which implies y=c+dx/b-da/b and thus y=(d/b)x+((bc-ad)/b) so d/b is the slope and (bc-ad)/b is the y-intercept of the line. Therefore, in our example, since the slope is 3 then d/b = 3/1 so d=3 and b=1. Since x=a+bt and y=c+dt, we can now say x=a+1t and y=c+3t. When t=0, x=a and y=c so (a,c) must be a point on the line. Let (a,c) = (7,5) so x=7+t and y=5+3t are the parametric equations for the line. A parametric sketch using NuCalc confirms our calculation.
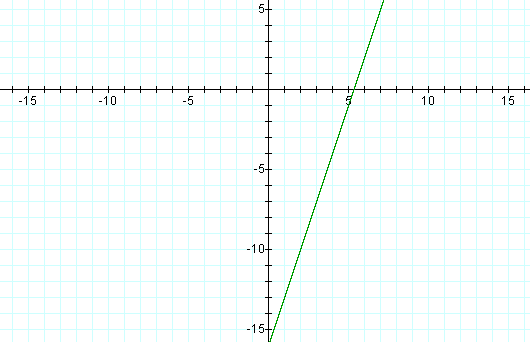
Notice the two graphs coincide, pass through the point (7,5), have a slope of 3 and a y-intercept of -16.