Explorations with Spreadsheets
EMAT 6680 - Assignment 12
by Mary Bruce
In this assignment the author will illustrate how spreadsheets (Microsoft Excel in this writeup) can be used to manipulate data and, in particular, create mathematical models for data to be used for regression analysis.
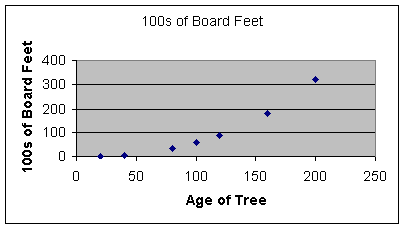
The following data represents lumber output per tree (in 100s of board feet) based on the age of the tree:
| Age of Tree | 100s of Board Feet |
| 20 | 1 |
| 40 | 6 |
| 60 | |
| 80 | 33 |
| 100 | 56 |
| 120 | 88 |
| 140 | |
| 160 | 182 |
| 180 | |
| 200 | 320 |
Typically when one first obtains data, a scatterplot should be generated to detect possible signs of a mathematical relationship:

At a glance one might guess that there exists a mathematical model to approximate this data. The shape of the graph hints at possibly an exponential or power function to better model the data.
First the author will attempt to fit an exponential curve to the data:
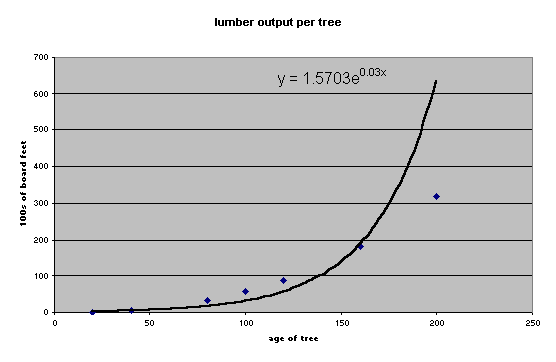
The curve fits closely for the lower numbers but as the age of the tree increases, the observed data does not increase at such a high rate ( notice the outlier at age 200). Notice the residuals (difference between observed and predicted values) for this model:
| Age of Tree | 100s of Board Feet | Residuals |
| 20 | 1 | -1.862 |
| 40 | 6 | 0.78509 |
| 60 | ||
| 80 | 33 | 15.682 |
| 100 | 56 | 24.44 |
| 120 | 88 | 30.488 |
| 140 | ||
| 160 | 182 | -8.993 |
| 180 | ||
| 200 | 320 | -314.3 |
One notices the exceptionally large residual at age 200 which contributes strongly to an average sum of squares of 14377.45776.
Indicators hint that a power regression model would probably serve the data better:
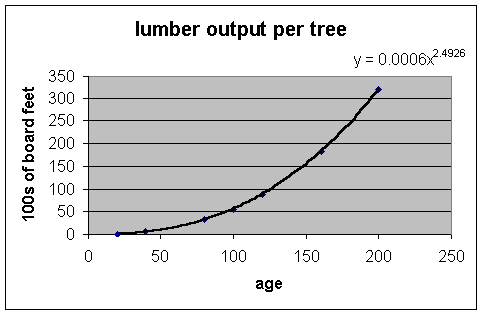
Notice how exceptionally tight the trendline fits the data points with very little residual error. Most likely this will serve as our best model for the data.
| Age of Tree | 100s of Board Feet | Residuals |
| 20 | 1 | -0.026 |
| 40 | 6 | 0.22586 |
| 60 | ||
| 80 | 33 | 0.50342 |
| 100 | 56 | -0.6756 |
| 120 | 88 | -1.282 |
| 140 | ||
| 160 | 182 | -0.889 |
| 180 | ||
| 200 | 320 | 1.0326 |
The mean sum of squares is a very low 0.6088090794.
Being careful not to extrapolate beyond our range of values we can now use the power model equation
y = 0.0006x^(2.4926)
to predict the lumber harvest for trees that are 60, 140 and 180 years old. The lumber output in 100s of board feet are 15.864, 131.11 and 245.296 respectively.