Tangent Circles
EMAT 6680 - Assignment 7
by Mary Bruce
The problem: Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
In this assignment the author will investigate three separate cases. Not only will the tangent circles be constructed but the locus of the centers of the tangent circles will also be examined.
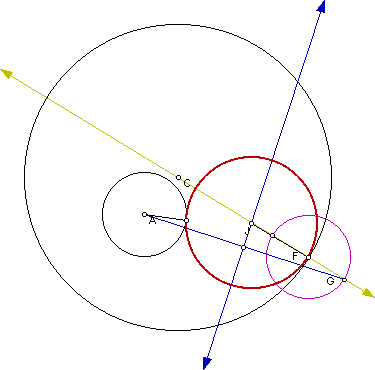
Case 1: Circle Inside Circle and Point of Tangency on the Interior Circle
Click here for a script to generate this sketch. The final drawing should look like the following:

Click here to trace the center J of all such tangent circles to the two given circles. We notice from the trace that the locus of centers of these tangent circles forms an ellipse with foci at the centers of the two original circles:

The locus of the centers is shown in green. Next we will examine the trace of the tangent line (in blue) to this ellipse.

Notice again the elliptical shape. Finally we will consider the locus of the midpoint of the segment that forms the base of the key isosceles triangle in the construction.
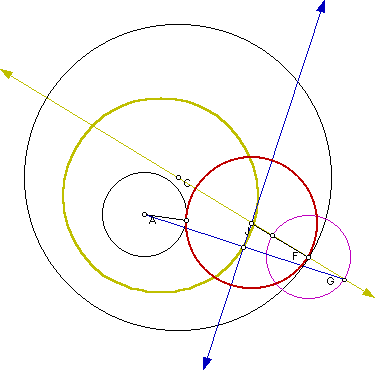
This locus almost appears circular with a center equidistant from the centers of the two original circles.
Case 2: Two intersecting circles
Click here to generate a script for this construction. The result should look like the following:
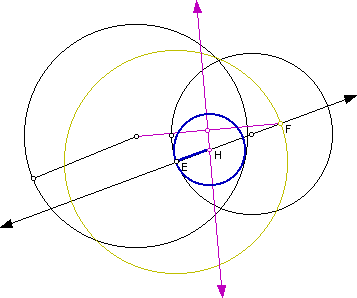
Next we will examine the locus of the centers of the constructed tangent circles. Click here to see a trace. Notice the trace in this case shows a hyperbola with foci at the original circle centers rather than an ellipse.
Case 3: Two Disjoint Circles
Click here to generate a script for this case. The result should resemble the following:
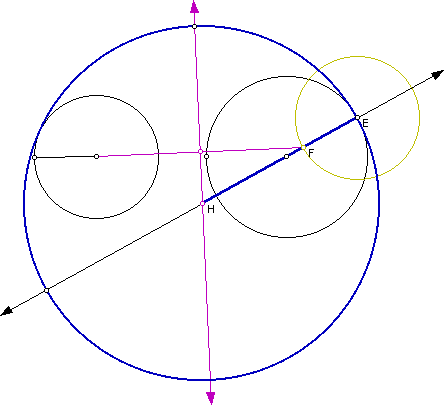
Notice the locus of the centers of the tangent circle is another hyperbola with foci that are the centers of the two original circles.
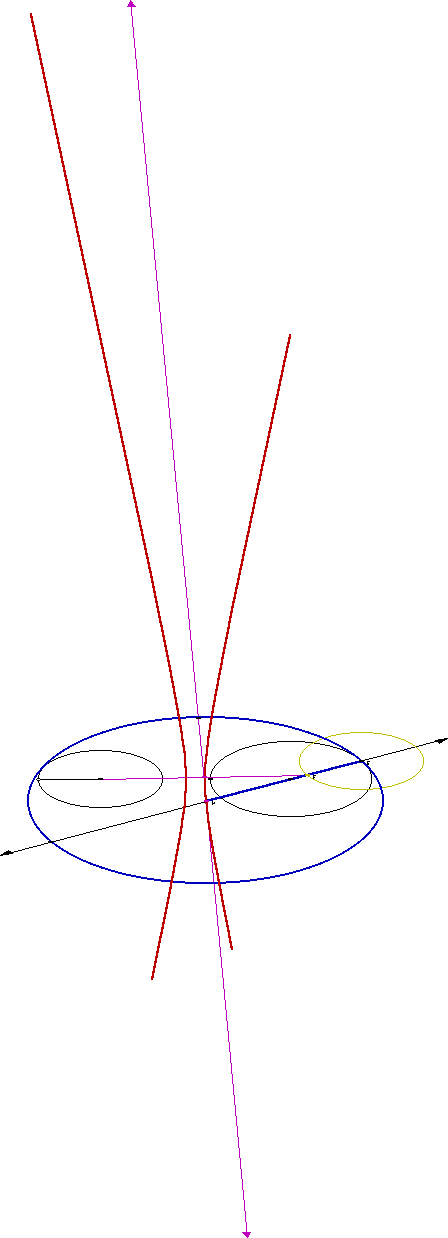
Throughout this investigation it became apparent that there exists many subcases of each of these cases sometimes even producing a different locus. One can explore these other possibilities making use of the GSP scripts. The author was only able to find loci of the tangent circle centers that were either ellipses or hyperbolas. No parabolas were discovered.