Altitudes and Orthocenters
EMAT 6680 - Assignment 8
by Mary Bruce
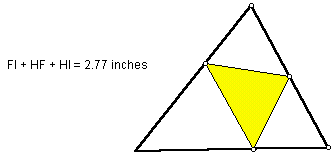
In this assignment, the author attempts to find the triangle of minimal perimeter that can be inscribed in a given triangle. Using GSP, one is able to translate vertices of the inscribed triangle and simultaneously record the perimeter. In doing this exploration, the author found the following results for a given acute triangle:

Looking at the picture, one can conclude the three vertices of the inscribed triangle appear to fall at the foot of the three altitudes. Construction of the three altitudes nearly confirms this conjecture:
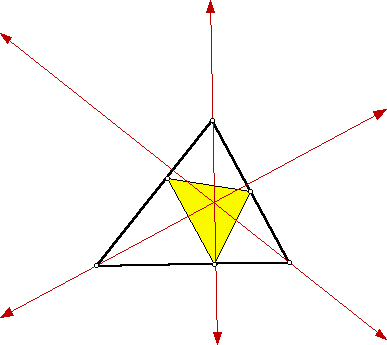
Should this conjecture prove to be true, one could conclude the orthic triangle(formed by connecting the feet of the altitudes) is the triangle of minimal perimeter that can be inscribed in a given acute triangle.
Given any acute triangle ABC and inscribed triangle TRP, reflect point P over segment AB and segment BC to get P' and P'' respectively:
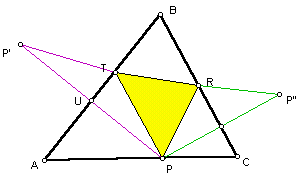
Since ΔP'TU is congruent to ΔPTU, we know segment P'T is congruent to segment PT. By the same reasoning, we have segment P''R congruent to segment PR so it follows that the distance from P'TRP'' is the same as the perimeter of inscribed ΔTRP. In order to minimize this distance between these four points, we would need them to be collinear as a straight line is the shortest distance between points.
It is important to find the placement of point P along segment AC so as to insure P'P'' is a minimum. ΔP'BT is congruent to ΔPBT and ΔP''BR is congruent to ΔPBR thus angle P'BP'' = 2· angle ABC from the original triangle.
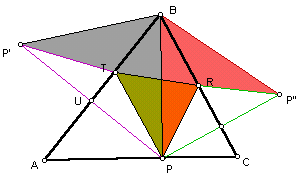
Since angle P'BP'' will always equal 2· angle ABC and since angle ABC remains the same since it is part of the original triangle, then all possibilities for ΔP'BP'' will be similar to each other by SAS Similarity. Since segment P'B is congruent to segment PB which is congruent to segment P''B, we want segment PB to be as small as possible to minimize segment P'P'' and thus know that it must be the perpendicular segment from B to P (an altitude). By a similar procedure, we could show that points R and T of the inscribed triangle must also be along the altitudes. Thus the orthic triangle is the triangle of minimal perimeter that can be inscribed in a given acute triangle.
One must question whether the same is true for right triangles and obtuse triangles. Given an obtuse ΔABC we notice the orthic triangle in red is no longer considered an inscribed triangle for ΔABC.
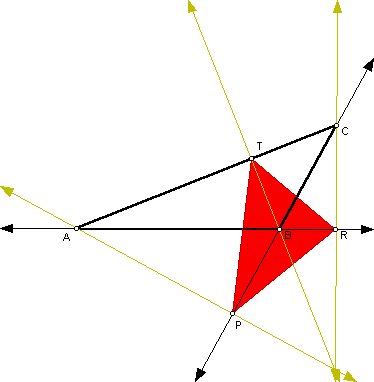
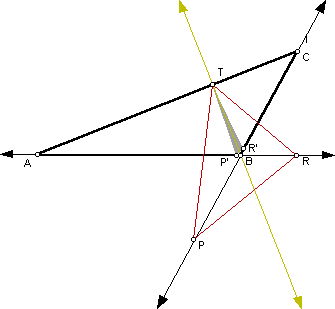
Through manipulation of the sketch, the author was able to conclude that the inscribed ΔPTR of minimal perimeter for obtuse ΔABC would be the triangle whose sides closely approach altitude BT, the only altitude that goes through the interior of the original ΔABC (labeled ΔP'TR' on sketch):
Similarly, the author discovered that the same is true for right triangles.
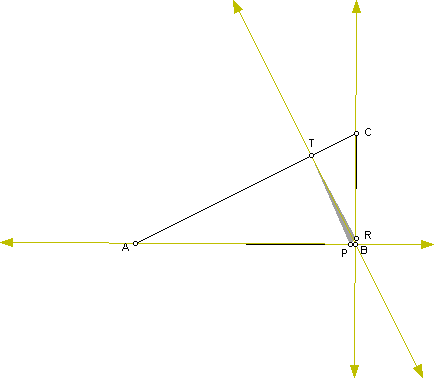
Thus the orthic triangle is the triangle of minimal perimeter that can be inscribed in a given triangle ONLY if that original triangle is acute.