Pedal Triangles
EMAT 6680 - Assignment 9
by Mary Bruce
In this assignment the author will explore pedal triangles based on various locations of the pedal point P. If P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of a given ΔABC is called the pedal triangle. Perpendiculars may also be constructed along the extension of a side if necessary.
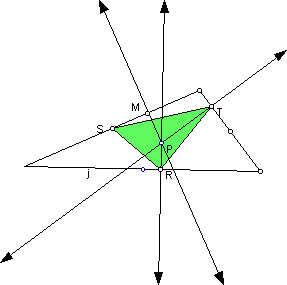
First, we look at the construction of a pedal triangle given that P is the centroid of the triangle:

Click here to manipulate a sketch for various types of triangles with the centroid as the pedal point. It appears that the pedal triangle never falls completely outside the original triangle. For acute and right triangles the pedal triangle falls inside the triangle but for obtuse it is partly inside the original triangle and partly outside.
Next we will explore the pedal triangle given that P is the incenter of the triangle:
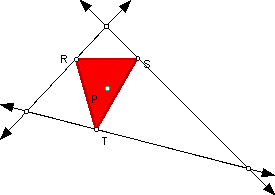
Click here to manipulate a sketch for various types of triangles using the incenter as the pedal point P. It appears that the pedal triangle will always be an acute triangle in this case and will always remain inside the triangle.
If P is the orthocenter of a triangle, we have the following sketch:
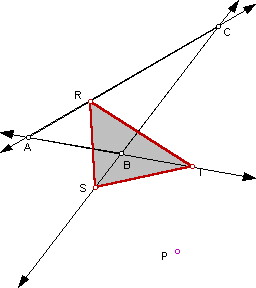
Click here to manipulate a sketch where pedal point P is the orthocenter. When P is in the interior of the triangle the pedal triangle remains inside the figure. As point P exits from a vertex the pedal triangle becomes degenerate and as P moves outside the triangle the pedal triangle is located partly inside and partly outside the figure.
Through this exploration the author discovered that degenerate pedal triangles are not limited to cases only when P is one of the vertices of the triangle. Further discussion on this SIMSON LINE is saved for a later investigation.
Next we will explore the pedal triangle given that P is the circumcenter of the triangle:
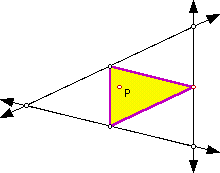
Click here to manipulate a sketch where P is the circumcenter of a triangle. It appears that when P is inside the triangle the pedal triangle is acute, when P is on the side of the triangle the pedal triangle is right and when P is outside the triangle the pedal triangle is obtuse. In all cases, however, the pedal triangle remains inside the original triangle.
Finally the author will explore an animation of pedal point P about the incircle of ΔABC. Traces of the midpoints of the pedal triangle will then be examined:
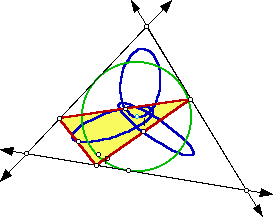
Notice the loci of the midpoints of the sides of the pedal triangle form three ellipses. Click here to view the traces.