The Graph of
EMAT 6680 - Assignment 2
by Mary Bruce
In this assignment the author examines multiple graphs of the
form 
for different values
of d.
The simplest form to look at would seem to be d=0. Thus, the
graph of the equation 
reduced to
is as follows:
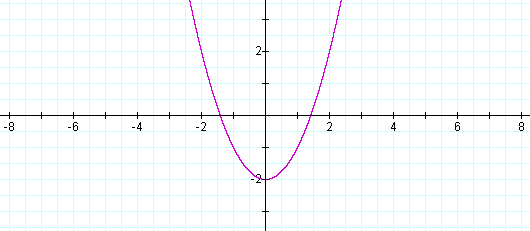
One notices the vertex of the parabola falls at the point (0, -2).
Next, choosing positive values of d (d=1,2,3,4) and producing graphs in sequential order to facilitate analysis of movement and change, one notices a horizontal translation of the graph d units to the right of the original.
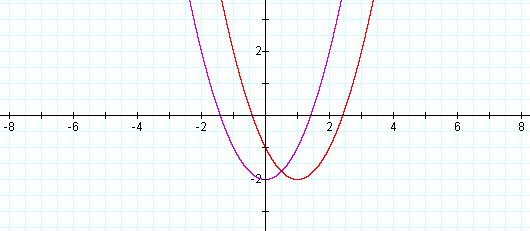
The vertex appears to have shifted to (1, -2) but otherwise no changes in the shape of the original graph are detected.
Looking at the graph of d=2,
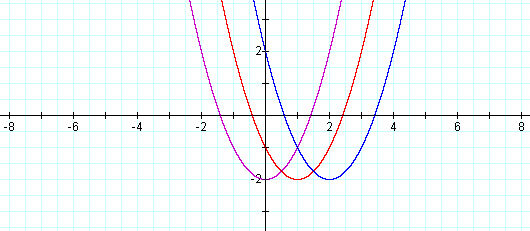
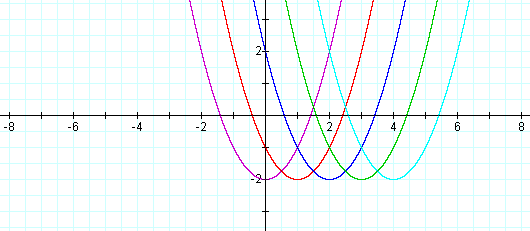
again no changes in the shape have resulted though the vertex has now shifted horizontally to the point (2, -2). The pattern continues for the graphs of d=3 and d=4:
Next, choosing negative values for d produces similar results. Using d= -1, we see a parabola with the same shape as the original shifted one unit to the left:
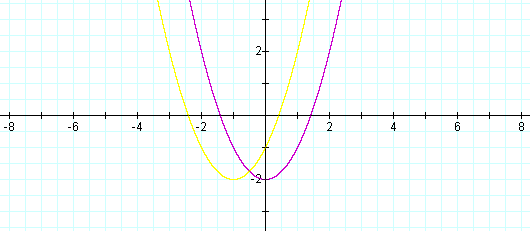
Notice the vertex has now changed to (-1, -2). Graphs using d=-2, -3, -4 are as follows and illustrate similar patterns as above:
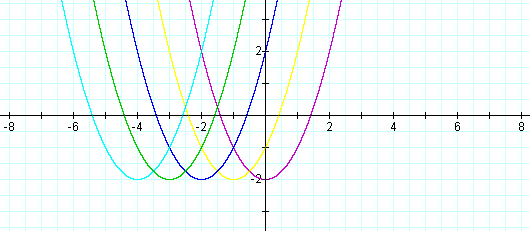
Even choosing fractional values for d produces expected results. Using d=1/2 and d= -1/2, we notices horizontal translations 1/2 units to the right and left respectively:
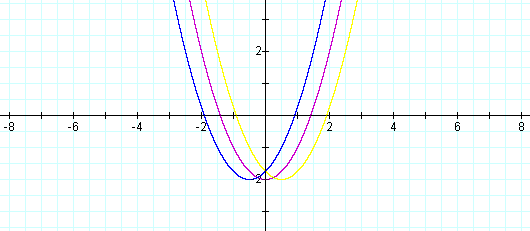
Analyzing the graphs and equations simultaneously, it is easy to conclude why this particular quadratic form is often referred to as VERTEX form:
y = (x - 0)^2 -2 vertex (0, -2)
y = (x - 1)^2 -2 vertex (1, -2)
y = (x - 2)^2 -2 vertex (2, -2)
y = (x - -1)^2 -2 vertex (-1, -2)
y = (x - -2)^2 -2 vertex (-2, -2)
Taking a quadratic equation
one completes the square
y = x^2 - 16x +64 +62
-64 to obtain
which should produce a parabola with
vertex (8, -2) that maintains the same shape as the original:
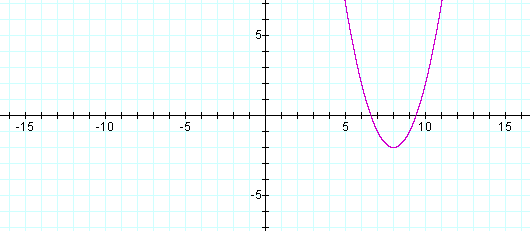
Click here to view a Nucalc animation of the discussed translation. You will need to hit the play button next to n at the bottom of the screen.