

First we want to construct a triangle ABC to start our exploration for today.
We now want to construct the orthocenter H for the triangle ABC. When we construct it it will look like this:
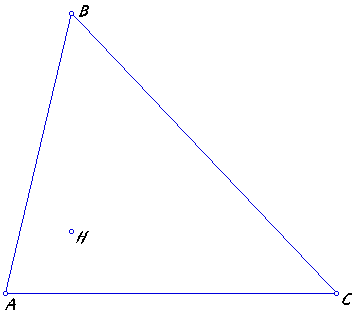
One observation that we can make is that the orthocenter H stays inside the triangle until it becomes a right triangle. When it is obtuse the orthocenter H will leave the triangle through the point A or the point C depending on which side the triangle will become obtuse.
We now want to construct the othorcenter of triangle HBC. So we will set the orthocenter H in the center of the big triangle ABC so that it will be easier to see.
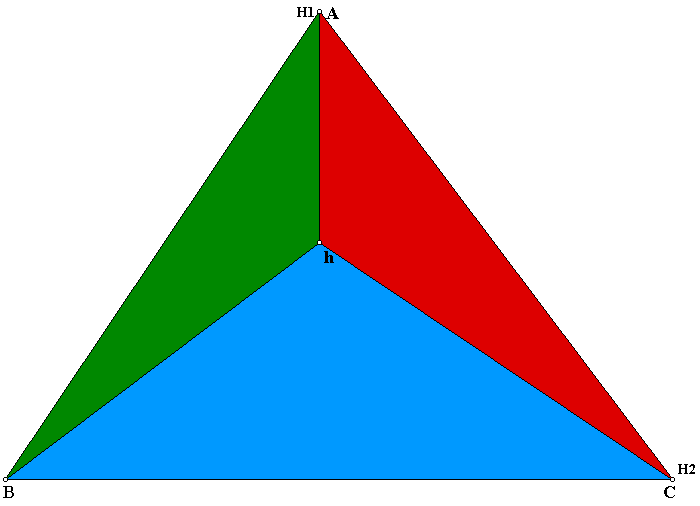
We can see that the orthocenter for the triangle HBC is the label H1 at the opposite vertex. So where will the orthocenter be for triangle HAB and HBC? Well we know they should be at the opposite vertices from each triangle. So lets see what it will look like when we have all the orthocenters for each of the smaller triangles labeled.
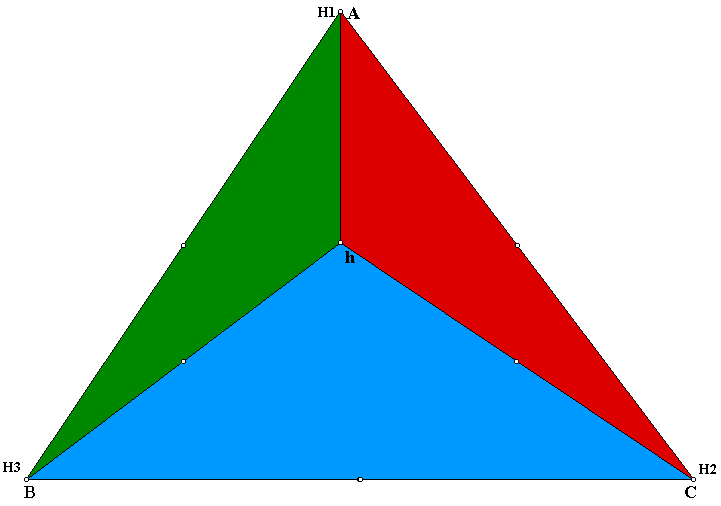
So we can see that the triangle HAC has an orthocenter H3 and at the vertex B and the triangle HAB has it's orhocenter H2 at the vertex C.
We now want to look at the circumcircles of each triangle. So we want to explore the HBC triangle first.
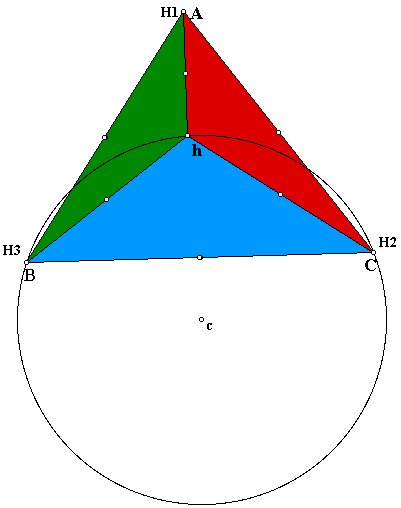
So we now want to compare the other three to this one and to each other. Lets now look at the circumcircle of triangle ABC.

So we see that the first two look close in size. Lets now look at the circumcircle for HAB.
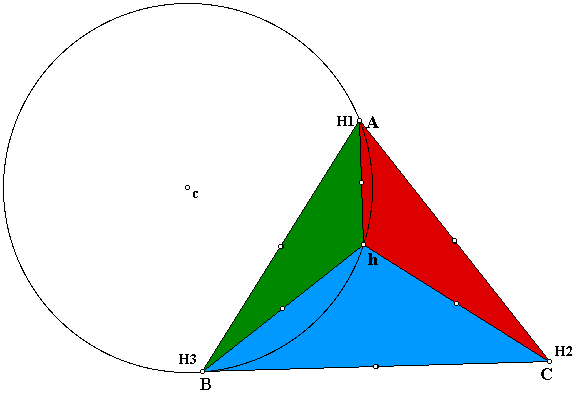
Finally, lets look at the triangle HAC. See if it is also close in size to the first three circumcircles.
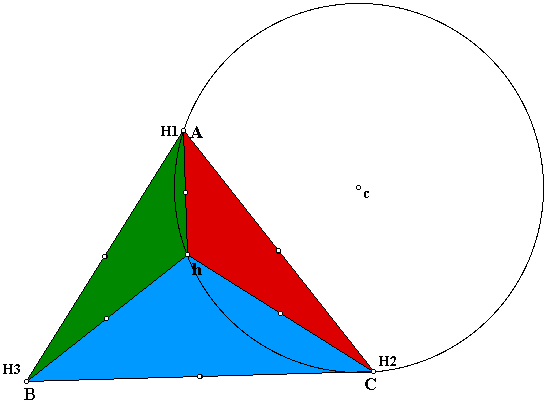
We see that all four circumcircles go through the three points of each desired triangle. So lets look at all four combined and see if this give us some more insight on if the four circumcircles of the four triangles are equal in size. We can draw points from the center of each circumcircle to each vertex and we see this gives us the following picture:

We see that each circle is close in size and with the lines we see we form a shape with around the triangle. One conjecture we can make is that each of the four circles is the same size. This is easier to see with the lines that we drew in the picture above.