

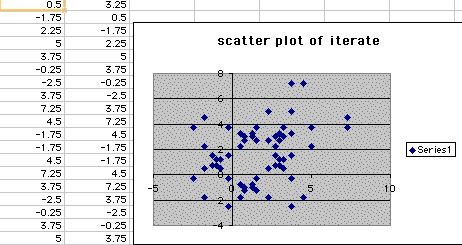
In using an excel spreadsheet to iterate numbers when a1=.5 and b1=3 and to see the different patterns the process will form when plotted on a scatter plot. We can see from the excel sheet below that when we iterate these numbers they give us a shape that looks similar to a gingerbread man.
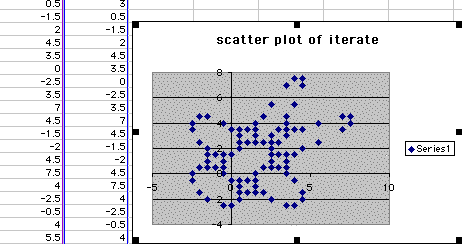
As we change inputs for B1 and keep A1 constant we can see certain patterns that take place when we place all of the outcomes on the scatter plot. It seems that we get the same gingerbread man when b1 is equal too2,2.5, 3, and 3.5. We also have close to another one when B1 is equal to 3.75, except the middle is missing from the body. We can also start with A1=.25 and b1=2.
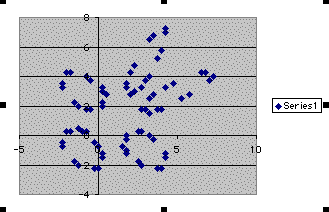
With this we get five seperate pieces,but when we change A1's value to .5 and leave B1 constant then this also gives us a gingerbread man.
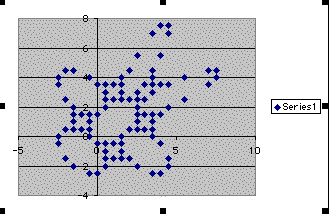
Lets see if we can determine a pattern that
they take when we start with our first set of values for A1 and
B1. We will want to leave A1=.5 and change B1 this time to determine
if and what the pattern might be. We see below at what we first
start out when we set B1=.25 and move up by .25 for each one.
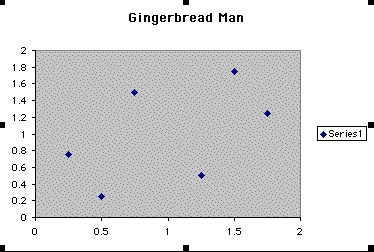
We see our first point at .5 for A and .25 for B. With this diagram the iteration pattern is all the same six points as we can see on the scatterplot above. A goes from .25 to 1.25 to 1.75 to 1.5 to .75 to .25 and back to where it began at .5. B goes from .25 to .5 to 1.25 to 1.75 to 1.5 to .75 to .25. So our pattern is repetitive over the 500 times with the same six spots in place.
We can try again with A=.5 and B=.5 to start off with. So since they are the same vale will we get only six points again with the difference in that B starts at .5? When we iterate we get the following:
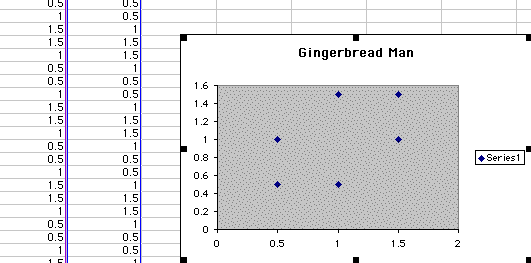
We can observe from the above scatterplot of the data that we do indeed get six points over and over throughout the 500 individual points. All that each can be is either .5, 1 or 1.5. So we have three data values that give us the same six points when we iterate.
For our next observation of the study we want
to see what happens when B is equal to .75. This gives us a scatterplot
after the iteration that looks like belo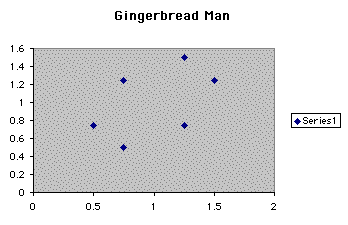
This gives us the six points again that are the same throughout the iteration.
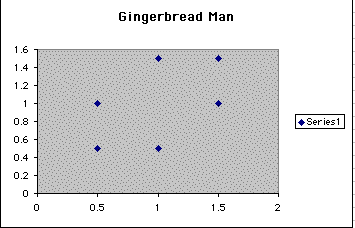
We can see that our first point when A is .5 and B is equal to 1 and the pattern goes counterclockwise from there for the six points in the scatterplot. So lets see if when B1 changes to 1.25 if this has any effect on the iteration pattern.
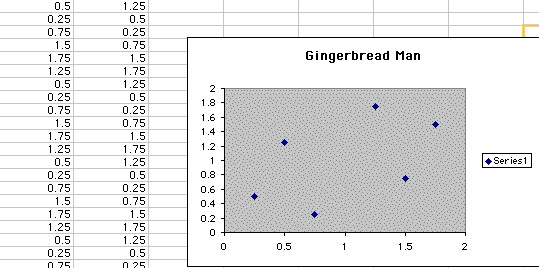
So we see that we are getting the same six points when we iterate the data for A=.5 and B =1.25. So we keep in mind that for when B is equal to 3 the scatterplot that we graph for the 500 points will give us the gingerbread man. So we keep on increasing B by .25 each time we iterate to see the pattern that is formed from the data.
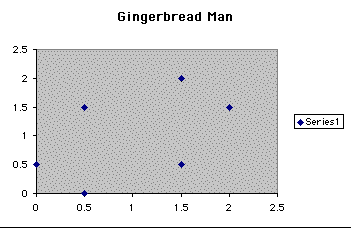
We see that this value gives us six points, but with the same points in each A and B. The plots can either be (0,0.5) or (.5,0), (1.5,.5),(.5,1.5), (2,1.5) or (1.5,2). Notice the leftward move of the scatterplot from the ones before. So we now want to investigate what the scatterplot will look like when B1 is equal to 1.75. Which will give us the following picture:
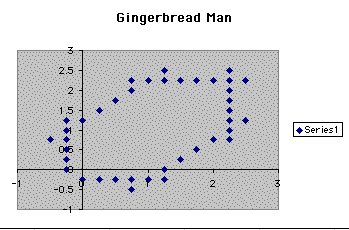
We first notice the change that takes place here as we now have 40 points over the 500 points of data. Also, notice how the figure has filled in and how the top and bottom mirror each other as we branch out in this mostly six-sided figure. We now know we are getting closer to the gingerbread man that first started our pattern.
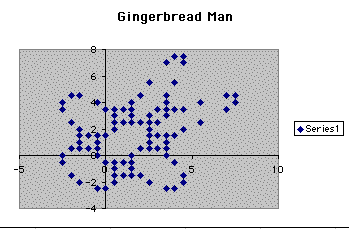
When the scatterplot is drawn it looks close to the gingerbread man that we started with if not the exact same except that B is equal to 2 and A is still kept constant at .5. It seems that the pattern starts over after 90 different data sets.
Lets now examine when B becomes 2.25. We can see below that the scatterplot is not a gingerbread man and that the repeating pattern starts over after 60 different sets of points.
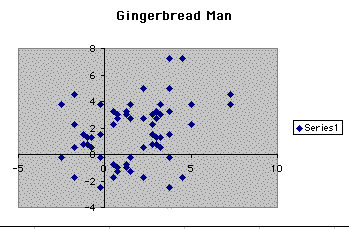
So we know that we are getting close to having the pattern go back to repeating after 90 different sets of points. So we explore and find that when B is equal to 2.5 that we have the following scatterplot.
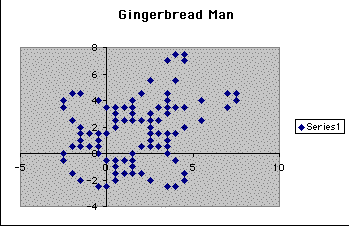
So we set B equal to 2.75 and know that it shouldn't go back to just 6 points for all 500 so we get the following plot:
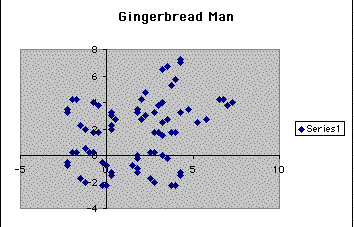
Notice that the pattern here repeats after 75 times. And we know the result of the picture below is that a gingerbread man will result when B is eqaul to 3 while leaving A constant at .5.
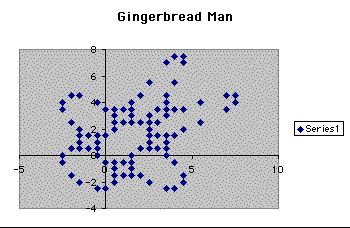
This gives us a gingerbread man that we first started out with where the pattern repeats after 90 different data sets. So we know what this gives us, but lets explore this idea a little more. So lets keep going up a little more for B1 while keeping A1 constant.
Notice how some of the shape is still there, but there are less points on the scatterplot. We can see that through the iterations that this pattern starts to repeat at (.5,3.25) after 60 different points. So lets move forward and try the next couple points for B1 to see if we can obtain a gingerbread man again. Letting B1 equal to 3.5 gives us the scatterplot below:
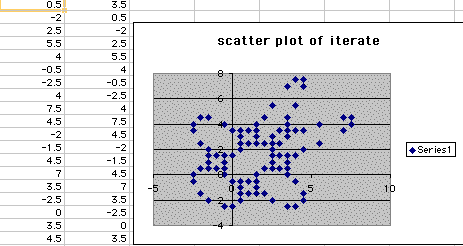
This again gives us a gingerbread man figure where the pattern is again repetitive for the 500 respective points after 90 different sets of points. So lets explore a couple more options for B1. Set B1 equal to 3.75 and we get the following scatterplot:
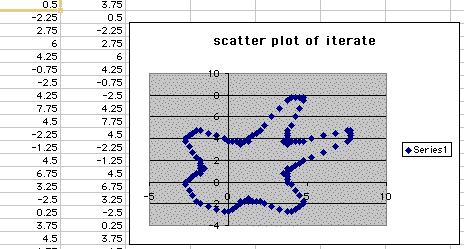
So we get the outline of the gingerbread man when B is equal to 3.75, but it does not give us the lines at the neck, arms and legs. If we can look at it from another angle it almost looks like an unfinished starfish with this scatterplot. So we want to inspect one more point that we can iterate. So we set B1 equal to 4.0. When we create a scatterplot of (.5,4) it gives us the following:
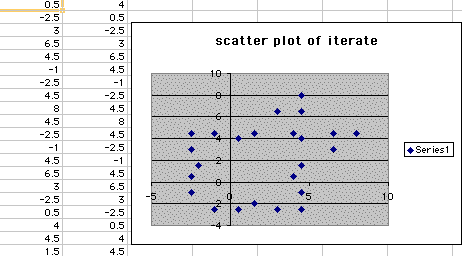
We see that it has about the same shape, but just with a more repeating pattern that gives us a lower number of different sets of numbers. This is an interesting concept that we can change A1 and keep B1 constant also. Here are some of the results of those in this picture below where A1 is equal to 4 and B1 is equal to 3.5 we get the following:
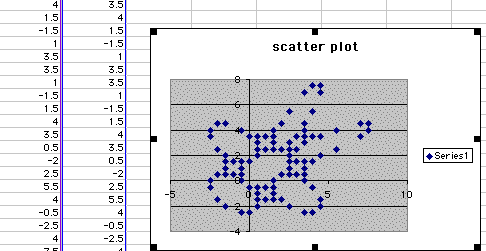
So we can form this pattern in many different ways through the iteration of two starting points to give us a gingerbread man pattern that starts repeating after 90 points, with other starting points giving us fewer sets of different points. If you would like to explore more here is a link to an excel spreadsheet that you can change A1 or B1 and see what kind of scatterplot will result from the two points.