

Today we want to explore different parametric
equations using Graphing Calculator with respect to COS and SIN
involved in today's equation. We want to see 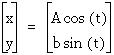 in
a graph as for t between 0 and two pi or approximately 6.28. We
will change the values in A and B to investigate what is going
on in today's assignment. Our first graph below is when A=5 and
B=1.
in
a graph as for t between 0 and two pi or approximately 6.28. We
will change the values in A and B to investigate what is going
on in today's assignment. Our first graph below is when A=5 and
B=1.

We can see that with this equation with A=5 it stretches the graph out along the x-axis. It becomes an oblong shape with B=1 also because it seems like from our first observation that B will coincide with the distance along the y-axis. Lets explore another graph to get a better grasp on it.
Lets see what it will look like when we keep A=5 and set B=3.

As we might have expected while making B larger it becomes more of an egg shape because when B is equal to three then it will grow taller on the y-axis.
So we can keep the same graph and see what we get when we set A and B equal to each other. What should we get? A circle would be a good assumption now that we see what is going on in the equation when we change variables A and B.
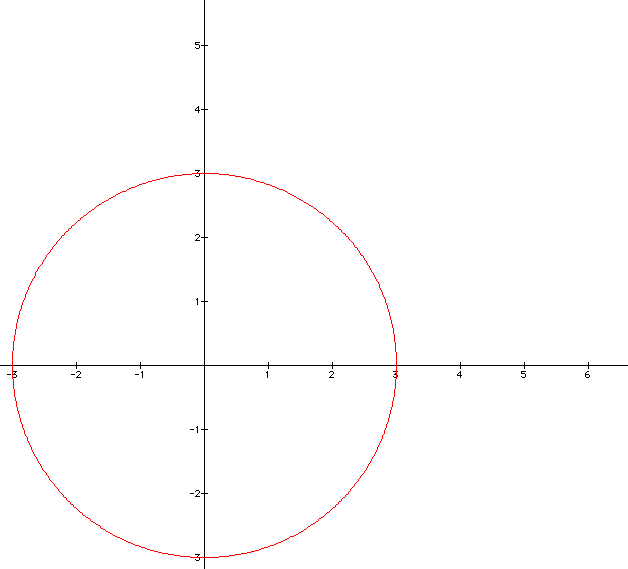
As we can see when A and B are set equal to one another in this parametric equation then we will get a circle as our graph.
We find out that as B gets larger we will move more along the y-axis than the x-axis. So lets make B=7 and keep A=5 which will give us the following graph:
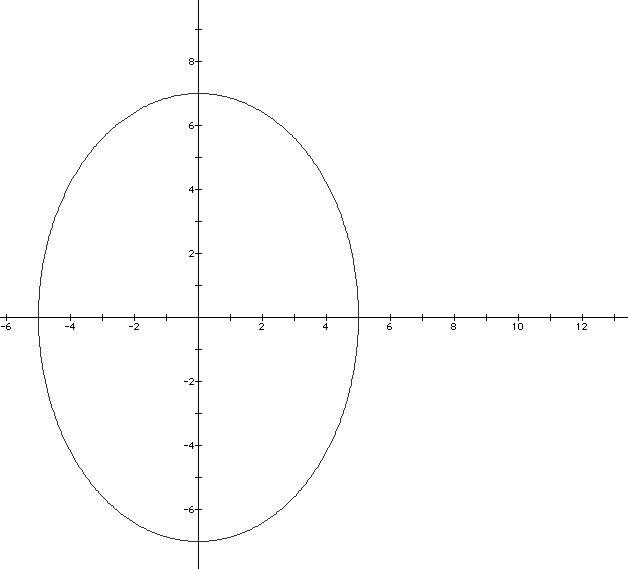
Now lets see the shapes as A is smaller than B which we would imagine to be similar to the equations before but now the objects should be stretched along the y-axis instead of the x-axis. So set A=2 and B=4 and we get this:

As we had thought the graph will go 4 down and 4 up along the y-axis corresponding to B and 2 positive and 2 negative along the x-axis corresponding to A.
We can stretch it out even further and let A=2 and B=7. We will get the following graph:

We see that the graph expands vertically with
B being larger than before. So through our investigations we can
now conclude that 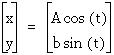 with t between
0 and 6.28 and being able to change A and B that with changes
to A we can reduce and expand it along the x-axis. Changes made
to B will allow us to reduce and stretch the shape long the y-axis.
So we should now be able to tell exactly what figure we will end
up with on the graph.
with t between
0 and 6.28 and being able to change A and B that with changes
to A we can reduce and expand it along the x-axis. Changes made
to B will allow us to reduce and stretch the shape long the y-axis.
So we should now be able to tell exactly what figure we will end
up with on the graph.
Whatever B is equal to the shape will correspond to the positive and negative of that number along the y-axis(vertical). Also, whatever A is set equal to, the shape will correspond to the positive and negative of that number along the x-axis(horizonal). So from now one when we are given this parametric equation we have a good idea of what the shape is going to look like on the graph.