

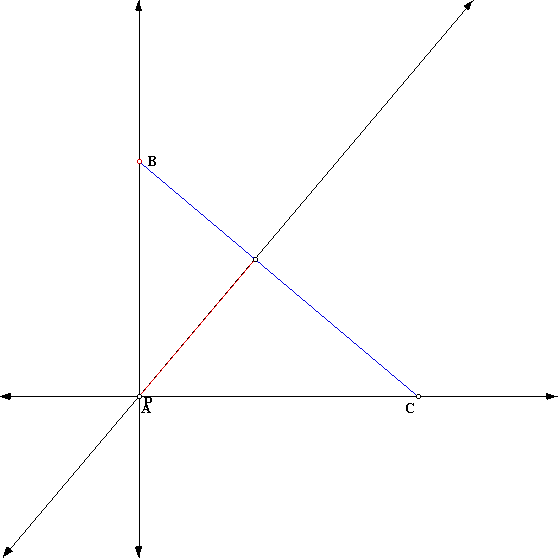
We will be looking at pedal triangles today. We will explore different options of some P(any point in the plane) and the pedal triangle RST for some point P. We first want to examine a point P outside of the original triangle ABC. So the picture will look like the following:
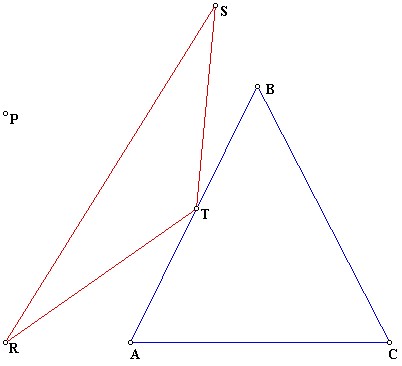
We now want to explore different options by moving P around to points such as the centroid, orthocenter, and circumcenter of triangle ABC.
First, we will examine when P is the centroid of triangle ABC. It will give us a triangle for point P like so:
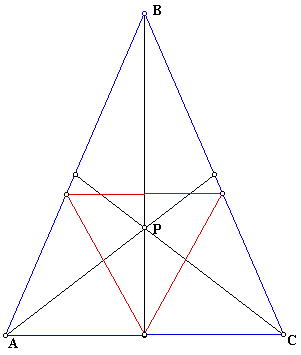
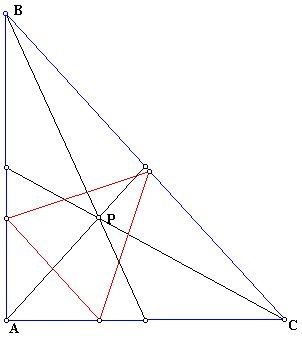
Here is another picture when ABC is a right triangle we see how the pedal triangle for point P changes:
We now want to explore the pedal triangle for P, when point P is the Orthocenter. When we create it starting near the middle of the triangle, lets see what it will look like:
How about when we have a right triangle and the Orthocenter will be on the vertex A? What will the pedal triangle look like then? It looks like this picture:
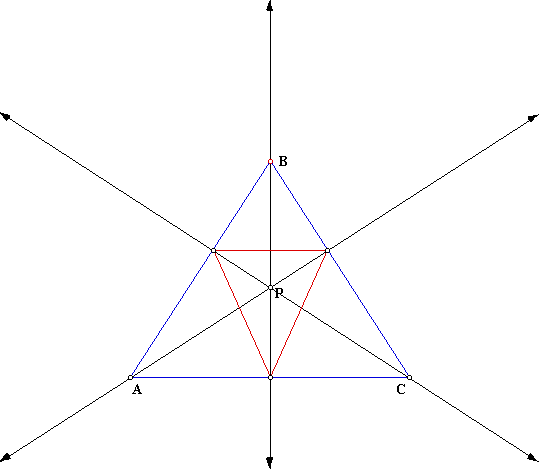
Lets explore the option of when the Orthocenter is outside of triangle ABC. It will give us the following picture:
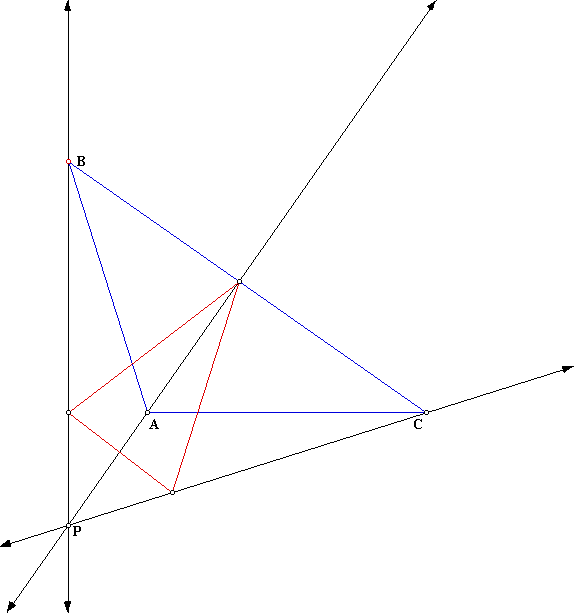
So we see that the pedal triangle when using P as the Orthocenter for an obtuse triangle ABC, will be centered about vertex A and point P will be outside of both triangles.
What would happen if P is the circumcenter of ABC? Well lets see what will happen to the pedal triangle then if will give us this picture:
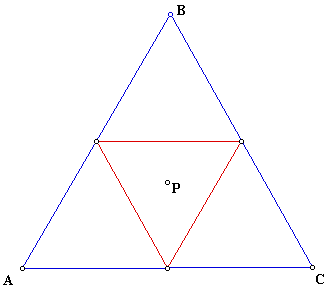
So we see that when P is in the center as the circumcenter it is inside both the pedal triangle and triangle ABC. What will it look like if we make ABC a right triangle? Lets now explore this option.
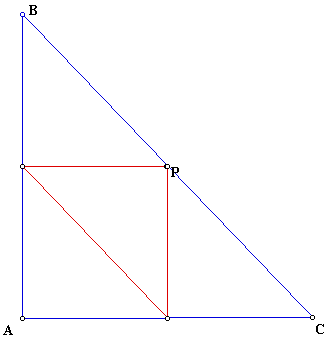
We see that P is at the midpoint of the segment BC. We can also observe that the pedal triangle is a right triangle inside of ABC when P is on the midpoint of BC. So what would we expect if ABC were an obtuse triangle? We should expect that P would leave both triangles and be on the outside. Here is a picture of it:
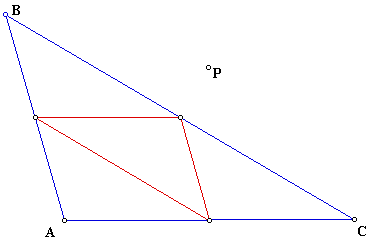
So we now know what will happen when P is a point outside the triangle ABC, or the Orthocenter, or the Circumcenter or the Centroid. We can use these observations to further our knowledge of the pedal triangle.