

We are going to explore several options on Graphing Calculator today and see the similarities and the differences between the graphs.
Lets first look at the graph ![]()
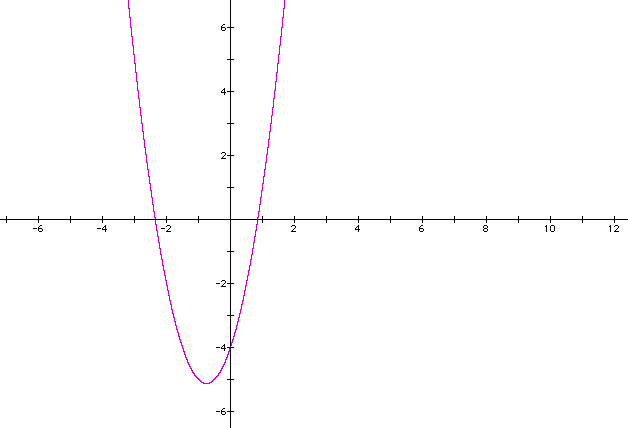
We now want to explore the differences between
the graph above and if we replace each x with (x-4). So lets look
at ![]() in red and the previous graph in
blue.
in red and the previous graph in
blue.
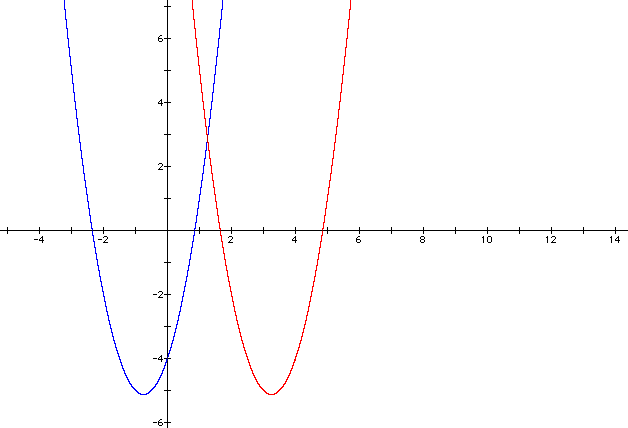
So they are both of the same shape with our
new red graph a little wider and it shifted four spaces to the
right along the x-axis. So we can consider adding a positive four
on the end and see if we can move it to the second quadrant. Lets
see what ![]() will give us when we graph it.
The graph of the equation will be in black.
will give us when we graph it.
The graph of the equation will be in black.
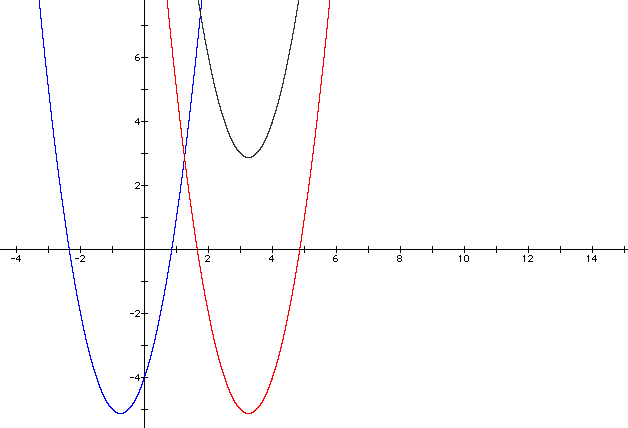
So we can visually see that it moves the graph
eight spots upward along the y-axis, but remains the same with
respect to the x-axis. This puts us in the first quadrant so we
know that adding four to the end of the equation will give us
a positive number corresponding to the y-axis, but we need a negative
number to correspond to the x-axis so that we can place the graph
in the second quadrant. So the last equation we will look at of
the four is ![]() . This will be the sky blue graph
in the picture below.
. This will be the sky blue graph
in the picture below.
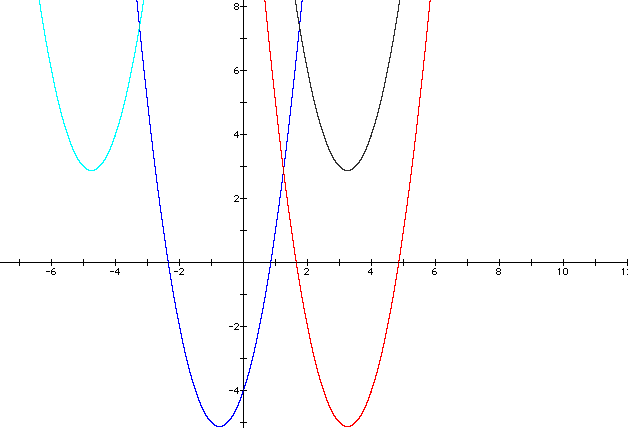
Well this picutre allows us to see what each part of the equation does to the graph. So to get the graph in the second quadrant we put a positive four inside of the parentheses and keep our positive four added to the whole equation. So it just moved 8 spaces along the x-axis while keeping the same height along the y-axis.
We know that both of the numbers outside the
parentheses have to be negative so that we can get a concave down
graph. So we want to keep the numbers inside the parentheses positive
so that we will get a graph in the second quadrant. So the first
equation we want to try is ![]() which
will give us a graph that looks like the following(the green color):
which
will give us a graph that looks like the following(the green color):
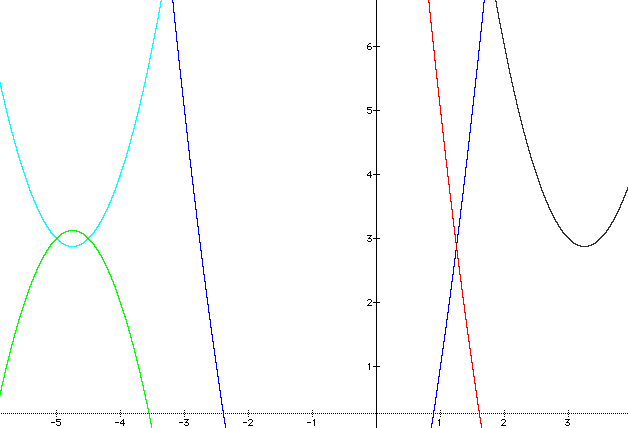
So we know we are close to the same vertex so it's probably not another whole number down so we'll try a positive 1.75 instead of 2 in our next graph.
Lets see if this will produce a graph that
is concave down that shares the same vertex. So we want to try
the following equation: ![]() to see if it shares
the same vertex in the graph below:
to see if it shares
the same vertex in the graph below:
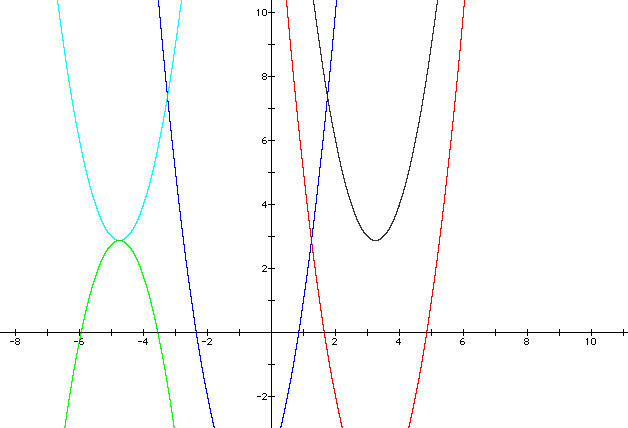
Well we can see that they meet at 3 on the y-axis and that the equation in the green graph will give us a concave down shape with the same vertex as the sky blue line in the previous equation.
Lets see if we can get one more eqution with
the same vertex. We think ![]() will
give us the same vertex as the red graph because there is a difference
of eight along the y-axis so we decrease our constant by eight
to give us a -6.25.
will
give us the same vertex as the red graph because there is a difference
of eight along the y-axis so we decrease our constant by eight
to give us a -6.25.
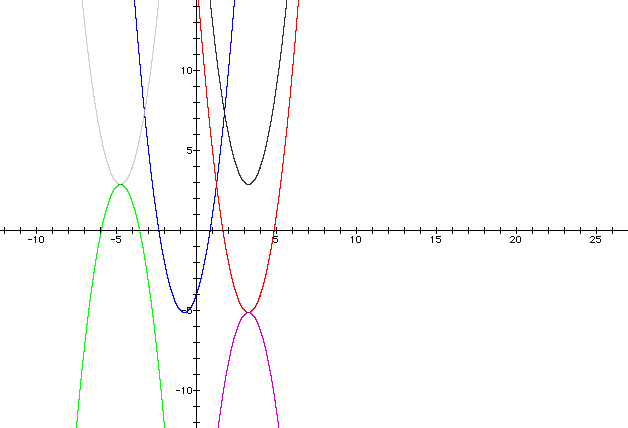
As we can see they do share the same vertex when we reduce the equation by eight and make the numbers multiplied by (x-4) the same numbers with a negative out in front of them. These explorations help us to see how the original equation changes when we throw in (x-4) into the new equations.