

We want to review some basic geometry before we go into more depth about it in a future assignment. Today, we want to explore the Orthocenter of a triangle. The Orthocenter of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. The Orthocenter(H) lies on the lines extended from the altitudes. We want to explore the location of the Orthocenter for different kinds of triangles. We will see where it is for an acute triangle, a right triangle, and an obtuse triangle. Do you have any idea where the Orthocenter might be when we have a right triangle? Well lets explore and find out exactly where it will be.
Lets first construct the Orthocenter by finding the common intersection of the three lines containing the altitudes for an acute triangle. It will look like this when we construct it:
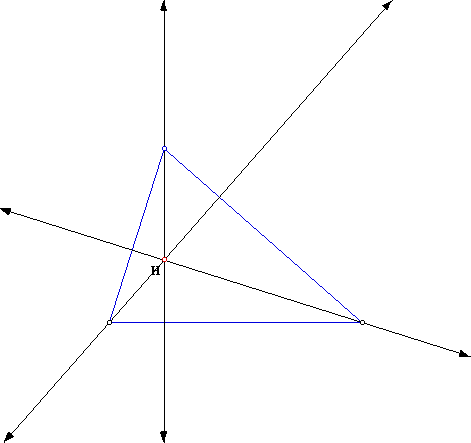
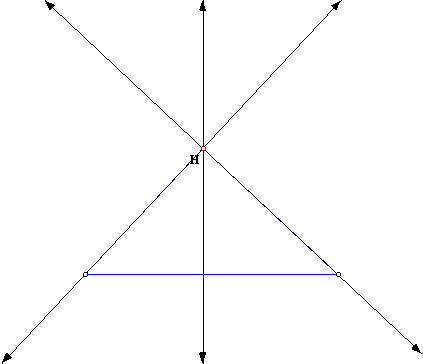
We find that the Orthocenter (H) is inside of the triangle for an acute triangle. So lets explore where it will be if all of the angles are close to sixty degrees. It will then look like the following:
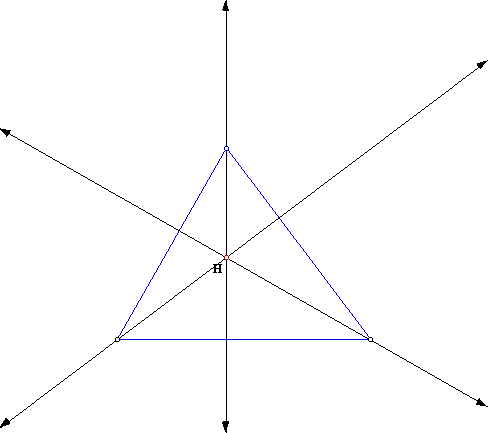
This gives us an Orthocenter location of close to the center of the triangle. We asked earlier where it would be located for a right triangle, so lets now explore this option. The triangle then will look like this:
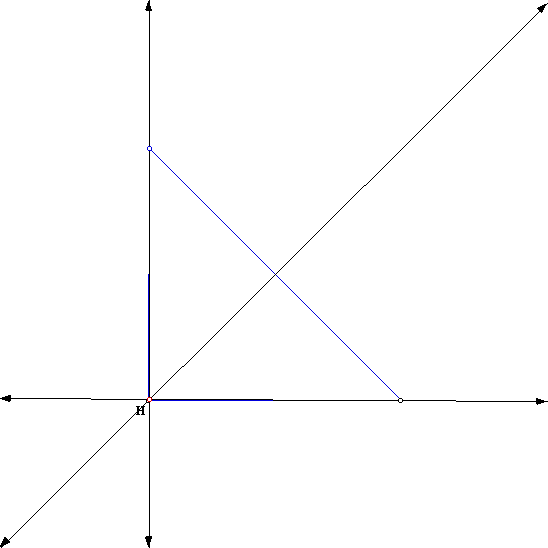
So the location for the Orthocenter for a right triangle is on the vertex. So what happens to the Orthocenter if we have an obtuse triangle? It has moved from the center of the triangle to the vertex as we have gone from an acute triangle to a right triangle. So this is what it will look like for an obtuse triangle:
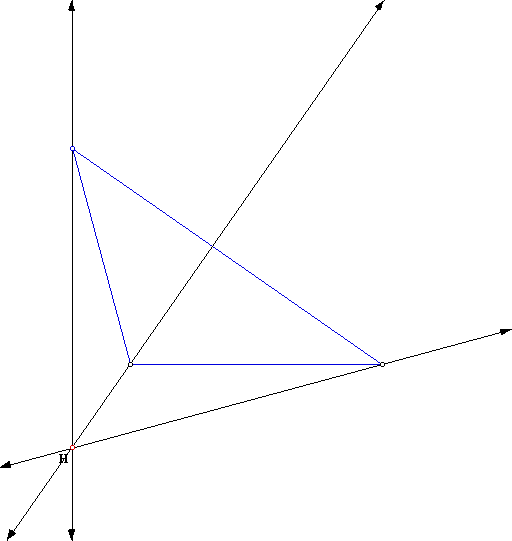
Now we observe that for an obtuse triangle, the Orthocenter will lie outside of the triangle. This will hold for the triangle whenever it is an obtuse triangle. Lets look at one further example. So when the top vertex of the triangle is a right angle we get the following triangle:
As we would expect from our earlier exploration the Orthocenter ( H) lies on the vertex. So the Orthocenter should go outside of the triangle if we make the angle obtuse. So when we make it an obtuse angle this is what the result turns out to be:
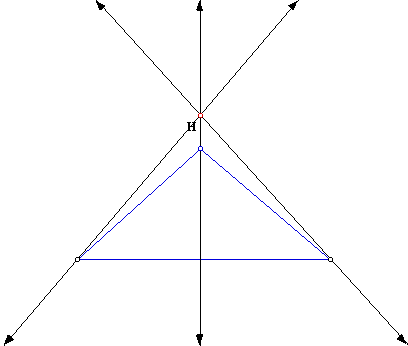
As we saw before the Orthocenter is outside of the triangle when the angle is obtuse. When the angle is acute, the Orthocenter lies inside of the triangle. A right triangle remember will have the Orthocenter on the vertex like so:
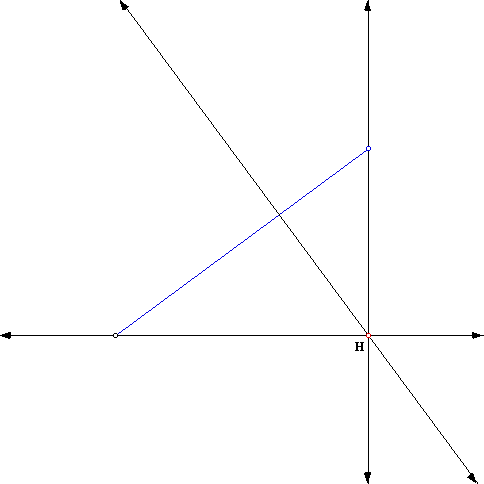
This will give us a better understanding of the Orthocenter and where it lies depending on the shape of the triangle that we are working with on the given assignment. We can explore futher options involving the Orthocenter and other elements of Geometry as we move through the semester.