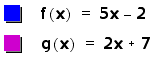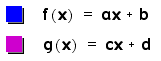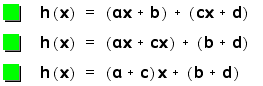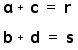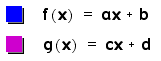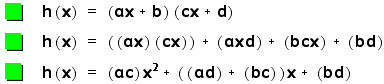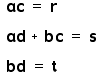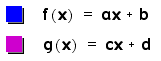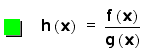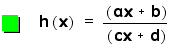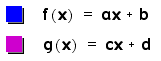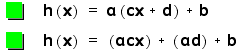Assignment #1
Explorering Linear
Functions
By: Elizabeth Gore
Assignment #1
Explorering Linear
Functions
By: Elizabeth Gore
In the following pages
we will investigate graphically what happens to linear functions
when they are added, multiplied, divided, and composed.
We will be working
with randomly selected functions for eachof these explorations.
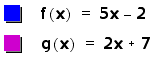
ADDITION
In the first case we
will look at the sum of the two linear functions.
Here is a bit of background
information about algebraically adding linear functions.
We will take the general
case for each function.
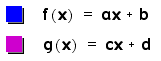 Where a,b,c, and d
are real numbers.
Where a,b,c, and d
are real numbers.
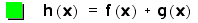 So, when we want to
form our new function, h(x), we will add these two function together
like so:
So, when we want to
form our new function, h(x), we will add these two function together
like so:
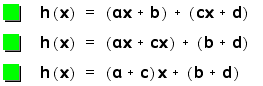 Since addition of real
number gives a new real number, we can substitute new letters
in to stand for the addition of the real numbers.
Since addition of real
number gives a new real number, we can substitute new letters
in to stand for the addition of the real numbers.
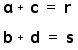 We get a new linear
function
We get a new linear
function
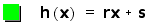 Let take a look graphically
at these linear functions.
Click HERE
Let take a look graphically
at these linear functions.
Click HERE
MULTIPLICATION
In this part of our
investigation, we will see what happens when we multiply linear
functions.
Again, it is helpful
to look at what happens algebraically before we look at graphs.
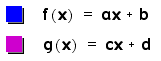 Where a,b,c, and d
are real numbers.
Where a,b,c, and d
are real numbers.
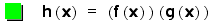 So, to form h(x), we
are going to multiply the functions:
So, to form h(x), we
are going to multiply the functions:
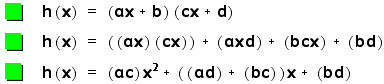 Since a,b,c, and d
are all real numbers, we know that musliplying them will give
us real numbers as well.
So, we could call the
product of these numbers seperate letters themselves. Doing so
will reveal something important.
Since a,b,c, and d
are all real numbers, we know that musliplying them will give
us real numbers as well.
So, we could call the
product of these numbers seperate letters themselves. Doing so
will reveal something important.
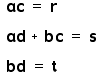 So now when we substitute
these letters for the numbers we would get when multiplying the
first real numbers we have:
So now when we substitute
these letters for the numbers we would get when multiplying the
first real numbers we have:
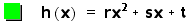 Hopefully this brings
back memories of the quadratic equation.
So you remember what
the graph of a quadratic euation looks like?
Click HERE to find out.
Hopefully this brings
back memories of the quadratic equation.
So you remember what
the graph of a quadratic euation looks like?
Click HERE to find out.
DIVISION
In this part of our
investigation, we will obviously be dividing our linear functions.
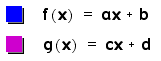 Where a,b,c, and d
are real numbers.
Where a,b,c, and d
are real numbers.
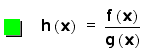 Looking at the general
case of h(x) does not reveal too much to begin with.
Looking at the general
case of h(x) does not reveal too much to begin with.
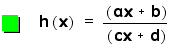 What we do know is
that cx+d can never equal zero, because division by zero is not
defined.
To investigate click
HERE.
What we do know is
that cx+d can never equal zero, because division by zero is not
defined.
To investigate click
HERE.
COMPOSITION
Finally, we have composition
of our two linear functions
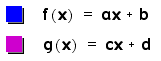 Where a,b,c, and d
are real numbers.
Where a,b,c, and d
are real numbers.
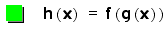 H(x) will show how
these general functions are conposed.
H(x) will show how
these general functions are conposed.
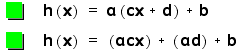 Since we have multiplied
and added real numbers, we can do as we did in the multiplication
section and gives those terms new names.
Since we have multiplied
and added real numbers, we can do as we did in the multiplication
section and gives those terms new names.
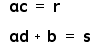 So we now have a function
that looks like
So we now have a function
that looks like
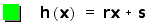 We get a new linear
function.
Want a better understanding?
Click HERE.
We get a new linear
function.
Want a better understanding?
Click HERE.
Return
to My HomePage