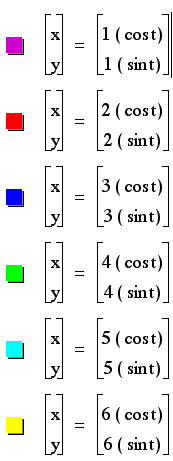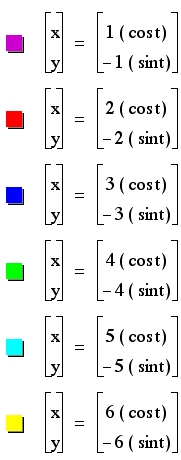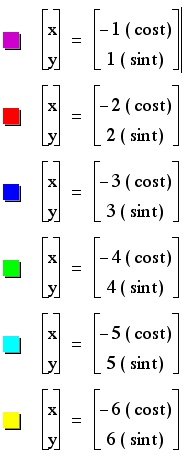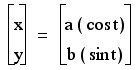Now we will look at
the cases when
a = b.
In this part of our
investigation of parametric equations, we will be using the parametic
equations
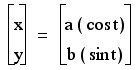 where
0 < t < 2Pi.
where
0 < t < 2Pi.
a = b
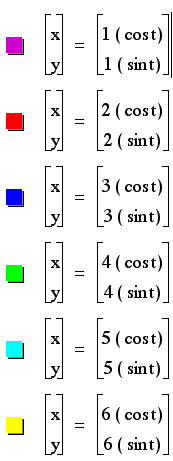
a = -b
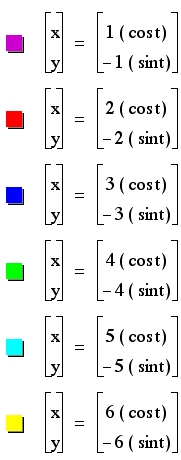
-a = b
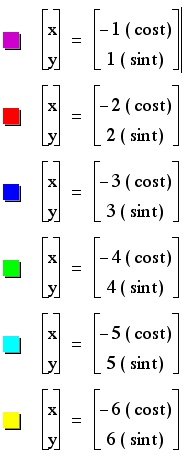
Conclusions:
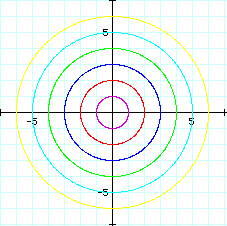
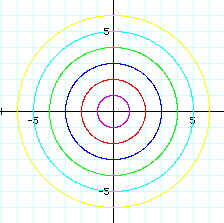
Notice that even though
we have changed the positive and negative values of each a and
b, the graphs remain the same.
Each graph crosses
the x-axis and the y-axis at a positive and negative a value and
a positive and negative b value.
So instead of looking
at the posasibilities when a
= b, it may be more fitting
to look at IaI = IbI.
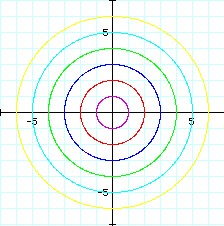
What we can tell from
the graphs, is that when evaluating the graphs of parametric equations
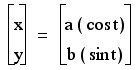 where IaI
= IbI,
we have a succession
of circles centered around the origin with the radii IaI
= IbI.
Return
to Investigation HomePage
where IaI
= IbI,
we have a succession
of circles centered around the origin with the radii IaI
= IbI.
Return
to Investigation HomePage
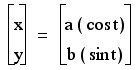 where
0 < t < 2Pi.
where
0 < t < 2Pi.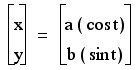 where
0 < t < 2Pi.
where
0 < t < 2Pi.