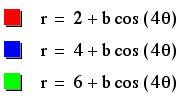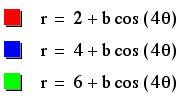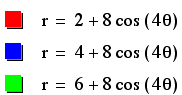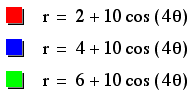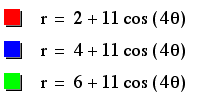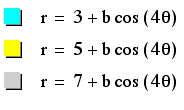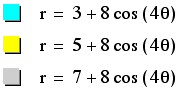Varying a
Even Variation
For this part of our
investigation, we will vary the value of a by even numbers while
keeping b and k constant.
Note: K will be kept
constant at 4. So, we know we will always have a four-petal symmetrical
rose.
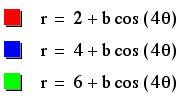
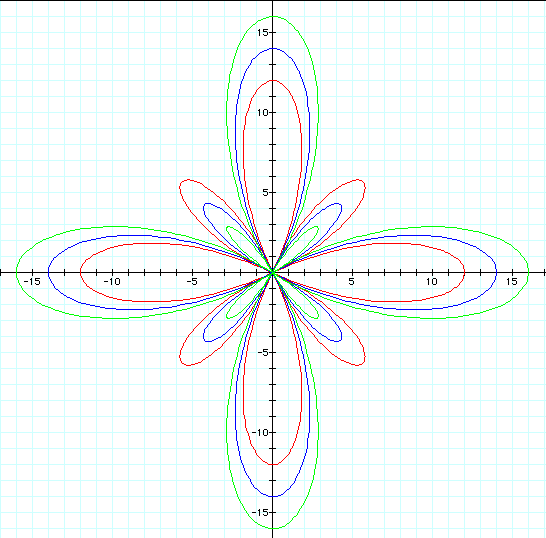
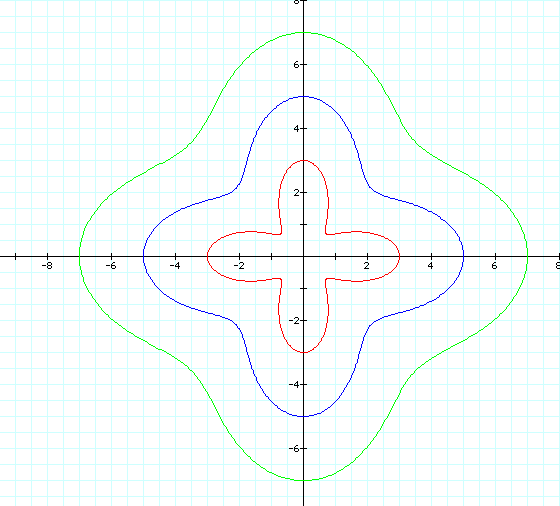We see that as a increases
on the even numbers, our rose becomes more spread out from the
origin, but it keeps its symmetry.
So now let's see if
we get the same expected results if b is larger than a.
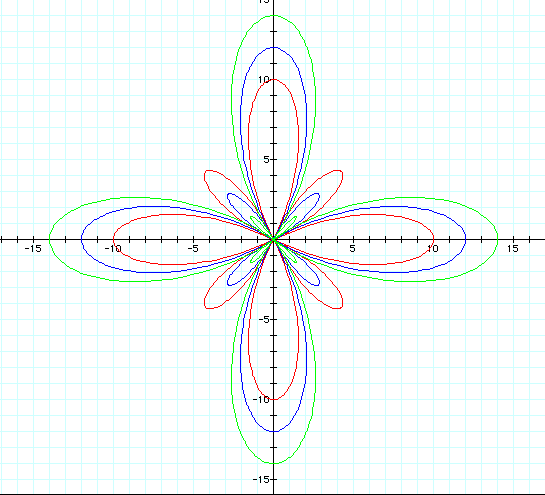What in the world have
we gotten here?
It looks like instead
of spreading our rose out, that it has pulled it in tighter to
the origin and doubled our number of petals for each flower.
It is worth testing
a few larger values of b to see if our observation is correct.
We will do so with
an odd and even value of b.
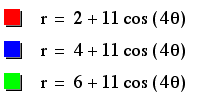
It looks like we are
right about the rose when b is larger than a.
But do we get something
different if a is odd?
Odd Variation
For this part of our
investigation, we will vary the value of a by odd numbers while
keeping b and k constant.
Note: K will be kept
constant at 4. So, we know we will always have a four-petal symmetrical
rose.
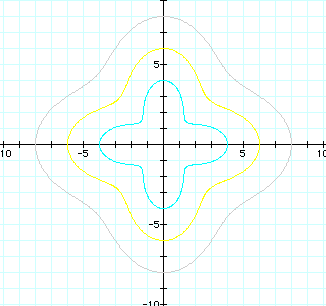It looks just like
the even graph, except that rose crosses the x and y axes at the
positive and negative even values immediately after the odd value
of a.
We see that our rose
is once again spreading out.
What if b is larger
than a?
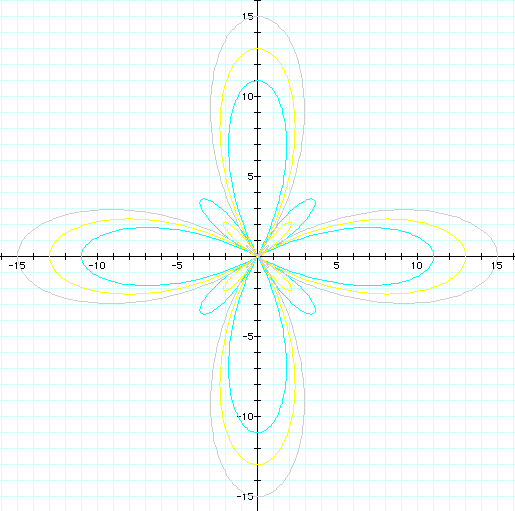Once again, we see
that same pattern for odd values of a.
We will assume that
the rose will result the same for any values of b which are larger
than a,
because it seems to
be following the same pattern as the even case.
Feel free to test it
on your own.
Return
to Main Investigation.