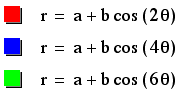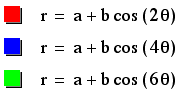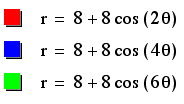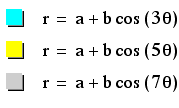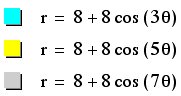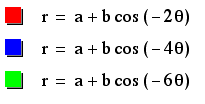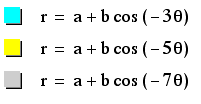Varying k
Even Variation
Let's take a look at
the first case. Here we hae kept a and b constant at 1 and varied
k by even increments.
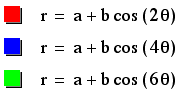
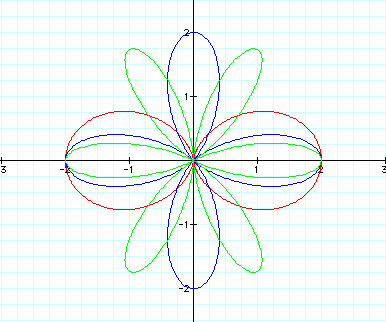 What do you notice?
We can see that the
number of petals on hte rose has changed as we vary k.
As a matter of fact,
the number of petals corresponds exactly to the value of k.
The petals seem to
be remaining symmetric.
What do you notice?
We can see that the
number of petals on hte rose has changed as we vary k.
As a matter of fact,
the number of petals corresponds exactly to the value of k.
The petals seem to
be remaining symmetric.
Above we only took
into account if a and b are less than k.
In this next graph
we see if there is any difference if a and b are greater than
k
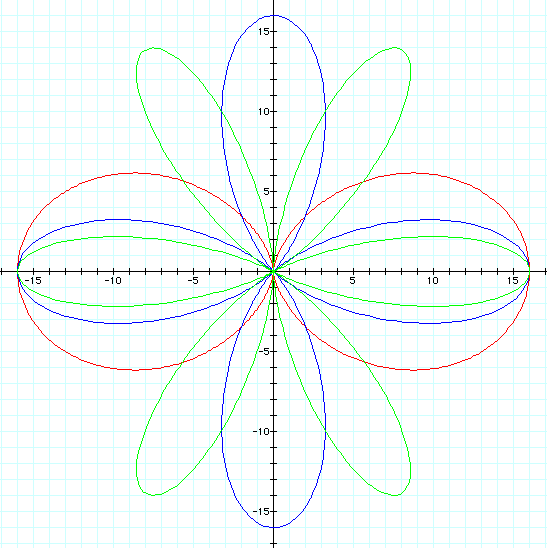 We still result in
a symmetrical rose with the number of petals equalling k, although
the petals are much larger.
We still result in
a symmetrical rose with the number of petals equalling k, although
the petals are much larger.
Generalization: When
a and b remain constant, and k is varied evenly, we will get a
symmetric rose with k petals
Odd Variation
Let's see what happens
when a and b remain constant, and k varies by odd numbers.
Our first example keeps
a and b constant at 1.
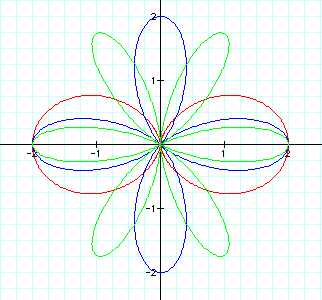
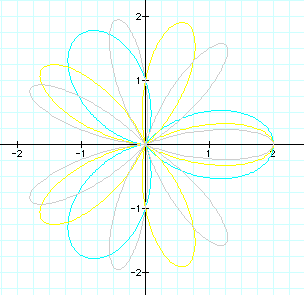 In the above graph
we can see that the roses do not remain symmetric, however k is
still equal to the number of petals.
In the above graph
we can see that the roses do not remain symmetric, however k is
still equal to the number of petals.
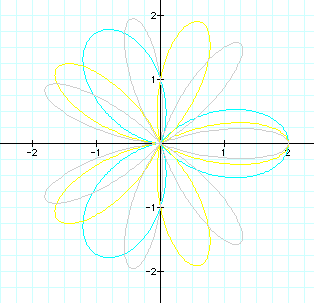
If we take into consideration
a and b values larger than k we get
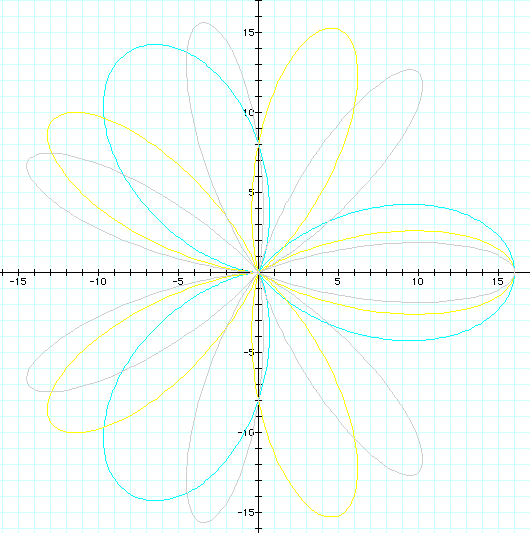 The same thing happens
with the odd values of k as with the even values.
The same thing happens
with the odd values of k as with the even values.
If k is an odd number
and a and b remain constant we will get a rose with k petals,
but it will not be symmetric.
We get the same results
for -k as we did above.
 Return
to Main Investigation
Return
to Main Investigation