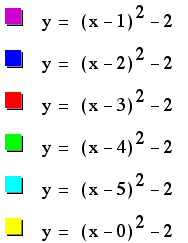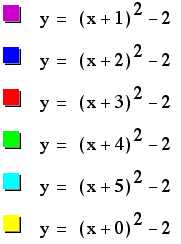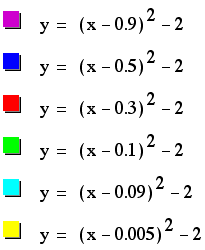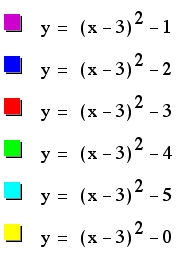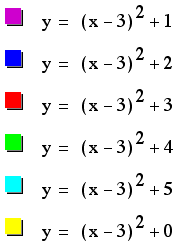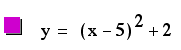Untitled Document

Assignment #2

Shifts of a Parabola

By: Elizabeth Gore

In this exploration we will be looking at a quadratic equation in the form of

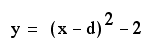What we would like to know is what happens to the graph of this equation when we vary d.

We should find out some interesting things about shifts of the parabola.

In the next few examples, we look at what happens to the graph of our equation when we change d.

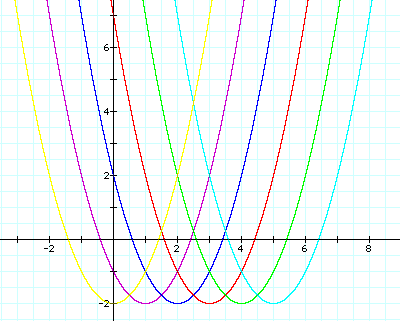
First, when we subtract positive values of d, we see that we will get a positive horizontal shift.

The shape of the parabola remains constant as well as the y-intercept of the vertex.

So, we can see that we are only changing the x-intercept of the vertex.

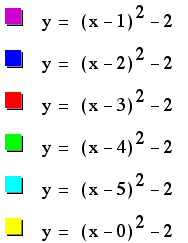
The same principle holds true for subtracting negative numbers (or adding positive numbers).

We know see a negative horizontal shift.

Notice, as in the first example, when d=0, our parabola's vertex lies on the y-axis, because we have had a 0 x-axis shift.

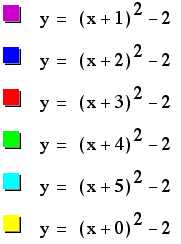
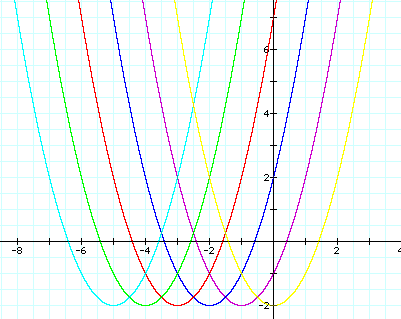
There is no difference when we do not use whole numbers, as shown below.

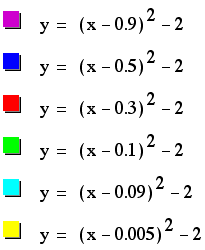
So, what can we say about d in the equation?

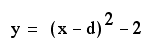D controls the horizontal shift, or the x-intercept, of the parabola, while everything else about the parabola remains constant.

But, let's make this a bit more interesting of an investigation.

How could we manipulate the vertical shift of the parabola with its structure remaining constant?

Let's look at this equation

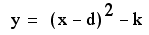If we keep d constant, perhaps at 3, we can vary K and see what happens.

In the next few examples, we look at what happens to the graph of our equation when we change k.

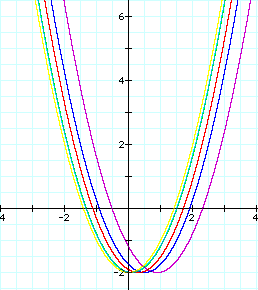
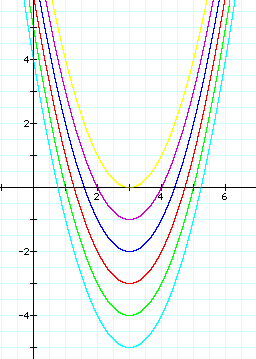
First, when we subtract positive values of k, we see that we will get a negative, vertical shift.

The shape of the parabola remains constant as well as the x-intercept of the vertex.

So, we can see that we are only changing the y-intercept of the vertex.

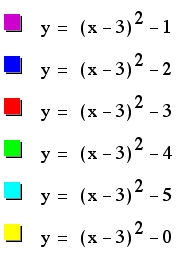
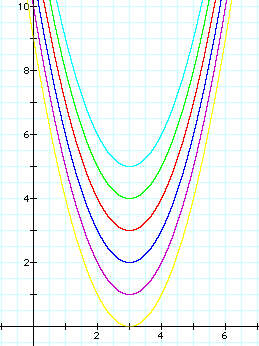
The same principle holds true for subtracting negative numbers (or adding positive numbers).

We know see a positive vertical shift.

Notice, as in the first example, when k=0, our parabola's vertex lies on the x-axis, because we have had a 0 y-axis shift.

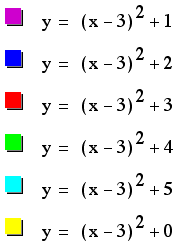
We can assume from this exploration that the vertex of the parabola given by this equation

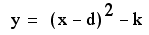can be manipulated horizontally and vertically by the d and k values given to it.

We have also learned how to know exactly where the vertex of a parabola given in this equation form lies.

EXAMPLE

Where does the vertex of this parabola lie?

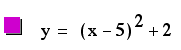If you guessed (5,2), you are correct.