ASSIGNMENT #4 - The Nine-Point Circle
Author : Elizabeth Gore
This particular investigation
will explore the existence of the Nine-Point Circle. To
adequately complete this task we must first take a quick look
at the definitions and circumcircles of each of these for the
same original triangle: Medial Traingle, Orthic Triangle,
and the Orthocenter Mid-segment Triangle. After overlaying
the circumcircles of each of the triangles listed above, you will
result with one beautifully presented circle, the Nine-Point
Circle. Each of the triangle's three vertices makes up one
of the nine points on the circle. Finally at the end of the investigation
I will provide a proof for the existance of the Nine-Point Circle,
so that you do not have to only take my word on it.
The Medial Triangle
The Medial Triangle
DEF of a given triangle ABC is constructed by connecting the midpoints
of the three sides of ABC. The circumcircle is constructed by
first finding the intersection of two perpendicular bisectors,
the circumcenter, which is the center of you circle. Then you
will use the distance from the circumcenter to a vertex of the
triangle as your radius. This process of finding the circumcirle
is the same for each of the three triangles we will discuss.
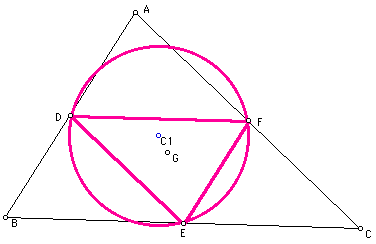In this graph the centroid,
intersection of the the medians of triangle ABC, is labled G.
The endpoints of these medians are the midpoints of the sides
AB, BC, and CA. Connecting these endpoints forms the medial traingle,
which we have labled DEF.
The circumcenter of
triangle DEF is labled as C1, since it is the first circumcenter
we have found.
The Orthic Triangle
The orthic triangle
of ABC is formed by finding the three altitudes. The altitude
extends from each vertex of the traingle ABC to the opposite side
at a right angle. The point on each side of the triangle where
these lines intersect form the vertices of the orthic triangle
pictured below.
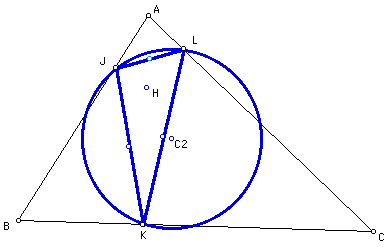The new found orthic
triangle is labled JKL. Within this triangle we have found the
orthocenter, labled H, which is the intersection of these earlier
stated altitudes.
Once again we use our
former method of finding the circumcircle on our new triangle
JKL.
The Orthocenter Mid-Segment
Triangle
The orthocenter mid-segment
triangle is a bit more difficult to understand, because it involves
finding both the orthocenter and then the midpoints between the
orthocenter and the original vertices. So, to begin with you start
your process as you would with the orthic triangle, by finding
the orthocenter, H, (intersections of altitudes). Once you have
done so, mark the midpoints between the orthocenter and each vertex,
or HA, HB, HC. These midpoints have been labled R, S, T, and will
be the vertices of your new triangle.
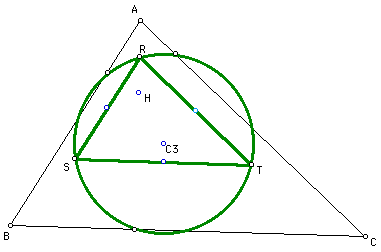After connecting the
midpoints, we have created the new triangle RST, which is the
orthocenter mid-segment triangle. The circumcircle can then be
constructed, just as before.
Overlaying the Circles.
If you look closely
at the above triangles ABC, you will notice that they are the
same triangle. We have found three new triangles with which the
circumcircle of each lies on the vertices of the respective triangles.
Let's look and see what happens when we put all of the NEW triangles
together within ABC.
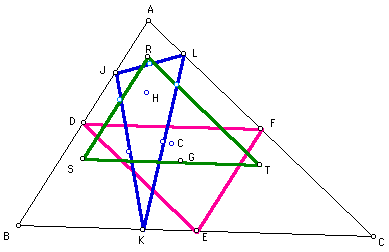What has happened?
Well, to begin with each of our circumcenters (C1, C2, C3) have
overlain each other to become one center, C. Since our circumcenters
are the same, we sould be able to deduce that the circumcircles
will be the same as well. Here is a picture.
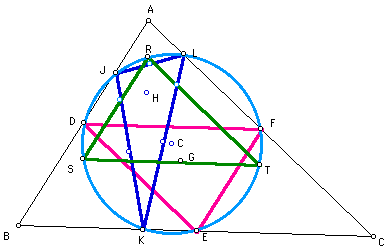So, now we have
The Nine-Point Circle!!
Here is a cleaner picture
without the triangle construction lines.
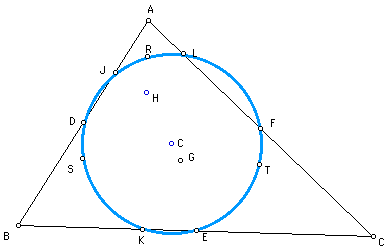
Think that thsi could
just be coincidence? Check out the PROOF (adapted from a proof on the website of the Computer
Science and Mathematics Depatment of Arkansas State University)
Back
To My HomePage