Proof of the Nine-Point Circle
The Theorum
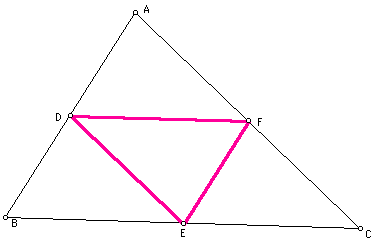
Given triangle ABC,
Let D be the midpoint of side AB. Let E be the midpoint of side
BC, and let F be the midpoint of side CA. (After connecting the
midpoints D,E, & F, the medial triangle DEF is formed.)
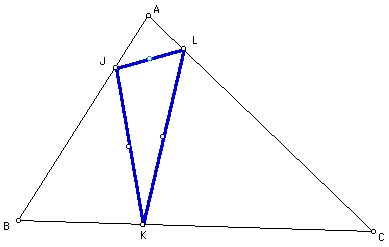
 Let point J be the
foot of the altitude from vertex C to side AB. Let point K be
the foot of the altitude from vertex A to side BC. Let point L
be the foot of the altitude from vertex B to side CA. (After the
feet of the altitudes are connected, the orthic triangle JKL is
formed.)
Let point J be the
foot of the altitude from vertex C to side AB. Let point K be
the foot of the altitude from vertex A to side BC. Let point L
be the foot of the altitude from vertex B to side CA. (After the
feet of the altitudes are connected, the orthic triangle JKL is
formed.)
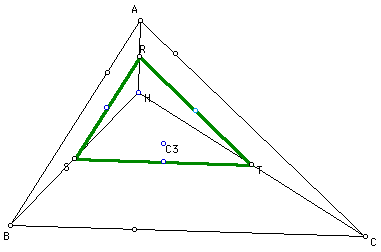
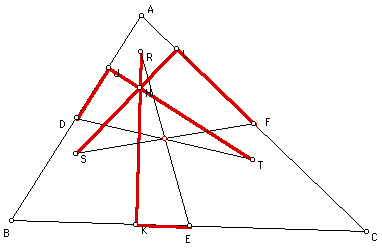
 If H is the orthocenter,
let point R be the midpoint of the segment AH. Let S be the midpoint
of the segment BH, and let T be the midpoint of the segment CH.
(After connecting points R,S, & T, the orthocenter mid-segment
triangle is formed.)
If H is the orthocenter,
let point R be the midpoint of the segment AH. Let S be the midpoint
of the segment BH, and let T be the midpoint of the segment CH.
(After connecting points R,S, & T, the orthocenter mid-segment
triangle is formed.)
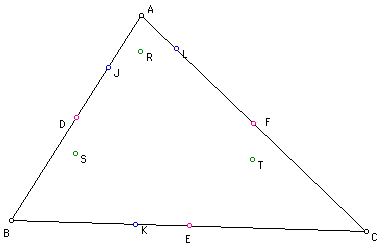
 We must prove that
points D,E,F,J,K,L,R,S, & T all lie on the same circle, ehich
forms the nine point circle of this triangle.
???
We must prove that
points D,E,F,J,K,L,R,S, & T all lie on the same circle, ehich
forms the nine point circle of this triangle.
??? ???
???
The Proof
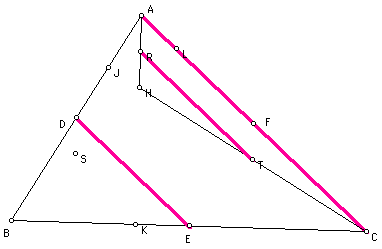
We have:
DE parallel to RT
How?? DE is parallel
to AC, because DE joins the midpoints of the two sides AB &
BC of triangle ABC.
RT is parallel to AC,
because RT joins the midpoints of the two sides AH & CH of
triangle AHC.
Therefore DE is parallel
to RT because they are both parallel to AC.
 We have:
DR parallel to ET
How? DR is parallel
to BH, because DR joins the midpoints of sides AB & AH of
triangle ABH.
ET is parallel to BH,
because ET joins the midpoints of sides CH & CB of triangle
CHB.
Therefore DR is parallel
to ET.
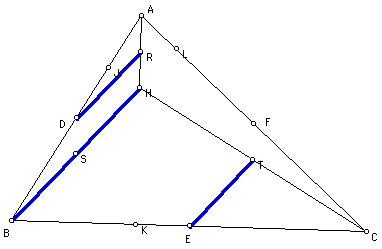
We have:
DR parallel to ET
How? DR is parallel
to BH, because DR joins the midpoints of sides AB & AH of
triangle ABH.
ET is parallel to BH,
because ET joins the midpoints of sides CH & CB of triangle
CHB.
Therefore DR is parallel
to ET.
 We have:
DR is perpendicular
to AC
How? From the proof
of DR is parallel to BH, we have that DR is parallel to BL, since
BL is a segment that passes through H.
Our theorum states
that BL is the altitude of the vertex B and the side AC, so from
the definition of altitude, we conclude that AL is perpendicular
to AC.
From the proof of DE
parallel to RT, we have that DE is parallel to AC.
Therefore we have DR
is perpendicular to AC.
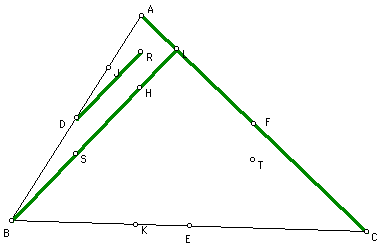
We have:
DR is perpendicular
to AC
How? From the proof
of DR is parallel to BH, we have that DR is parallel to BL, since
BL is a segment that passes through H.
Our theorum states
that BL is the altitude of the vertex B and the side AC, so from
the definition of altitude, we conclude that AL is perpendicular
to AC.
From the proof of DE
parallel to RT, we have that DE is parallel to AC.
Therefore we have DR
is perpendicular to AC.
 Now, we have that,
when the points are connected, DERT forms a rectangle. Similarly,
DFTS forms a rectangle, as well.
We can see that the
segment DT lies on the diagonal of both of the rectangles, passes
through the center of the circle and connects points on the circle.
Therefore DT is the diameter of the circle.
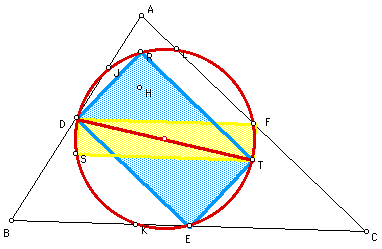
We now have that D,E,F,R,S,
& T are all points on the circle with the diameter DT. Sincle
DT is the diagonal of both rectangles, the six points at the vertices
of the rectangles are equidistance from hte midpoint of DT.
Now, we have that,
when the points are connected, DERT forms a rectangle. Similarly,
DFTS forms a rectangle, as well.
We can see that the
segment DT lies on the diagonal of both of the rectangles, passes
through the center of the circle and connects points on the circle.
Therefore DT is the diameter of the circle.
We now have that D,E,F,R,S,
& T are all points on the circle with the diameter DT. Sincle
DT is the diagonal of both rectangles, the six points at the vertices
of the rectangles are equidistance from hte midpoint of DT.
 Since segment CJ is an altitude of
the triangle ABC, J is on the circle with diameter DT.
The same for points L and K. They are
both the feet of the altitudes of different sides of triangle
ABC.
So, L and K will lie on the circle,
as well.
Since segment CJ is an altitude of
the triangle ABC, J is on the circle with diameter DT.
The same for points L and K. They are
both the feet of the altitudes of different sides of triangle
ABC.
So, L and K will lie on the circle,
as well.
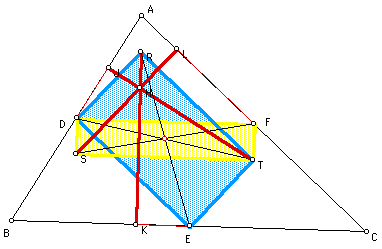 Angle TJD is a right angle. Since the
diameter DT subtends the right angle at J, J must be on the circle.
This argument can be similarly made
for points K and L.
Angle TJD is a right angle. Since the
diameter DT subtends the right angle at J, J must be on the circle.
This argument can be similarly made
for points K and L.
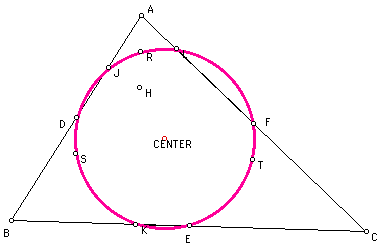
 Finally we have the proof of the nine
point circle.
Finally we have the proof of the nine
point circle.
 Back
To Investigation
Back
To Investigation




 ???
???





