Assignment # 6

The Locus of a Vertex

By : Elizabeth Gore

---

The problem we will be exploring in this investigation is:

HOW CAN WE FIND THE LOCOS OF A POINT WHEN GIVEN TWO VERTICES AND THE ANGLE

AT THE THIRD VERTEX OF A TRIANGLE ABC ??

---

First we will begin by constructing the triangle ABC with the circumcenter and circumcircle.

I have also gone ahead and connected the vertices to the circumcenter, C1.

---

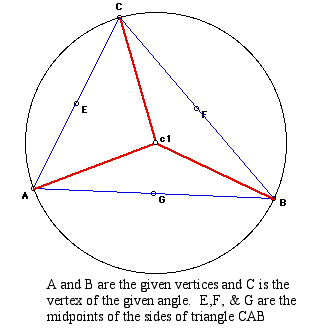
Using our knowledge of triangles and circumcenters, we know that c1 is equidistance from each of the vertices.

So we have d(Ac1) = d(Bc1) = d(Cc1).

It is easy to infer that triangle ABci is an isosceles triangle, because we know that d(Ac1) = d(Bc1)

The Isosceles Triangle Theorum tells us that since d(Ac1) = d(Bc1),

then the measurement of angle (c1AB) must equal the measurement of (c1BA).

If we think about it carefully, we can call these angles the same angle when speaking of measurements.

So, we can conclude that 2m(c1AB) + m (Ac1B) = 180 degrees. (Triangle sum Theorum)

Similarly, we can show that 2m(CBc1) + m(Cc1B) = 180, and

2m(CAc1) + m(Cc1A) = 180.

The actual angle measurements are listed below the sketch.

---

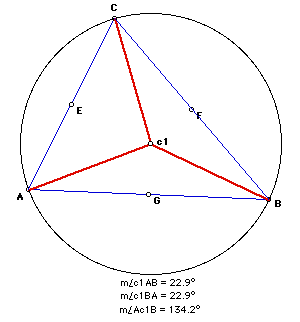
Just as we saw with triangle Ac1B, we can apply the Triangle Sum Theorum to triangle ACB.

m (ACB) + m(CBA) + m(BAC) = 180 degrees

---

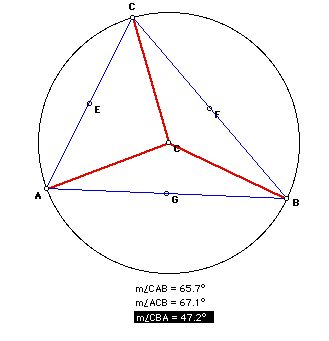
Since we know that angle measure is additive, we can conclude the following:

m(CAB) = m (CAc1) + m(c1AB)

m(ABC) = m(ABc1) + m(CBc1)

m(BCA) = m(BCc1) + m(c1CA)

Now it is fitting for us to say that

2m(c1AB) + 2m(c1BC) + 2m(c1CA) = 180 degrees

The actual angle measurements are listed below. I will leave the computation for you!

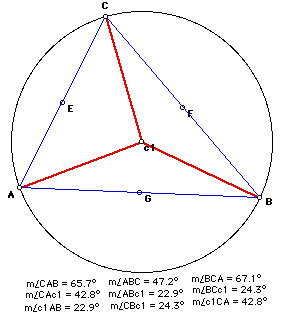We can see from the above picture that

m(Cc1A) + m(Ac1B) + m(Bc1C) = 360 degrees

With some rearranging we get:

m(Ac1B) = 360 - m(Cc1A) - m(Bc1C)

m(AciB) = 360 - (180 - 2m(c1CA)) - (180 - 2m (BCc1))

m(AciB) = 2(m(c1CA) + m(BCc1))

From our investigation, we saw that

m(BCA) = m(BCc1) + m(c1CA)

So through manipulation of the different angle equalities, we get that

m(BCA) = m(c1BC) + m(c1CA)

Therefore:

m(Ac2B) = 2m(ACB)

---

Keeping in mind the knowledge we have built up to, it follows that for any point H on the given circle,

which is on the same side of the chord AB as point C, with H not C,

m(Ac1B) = 2m(AHB).

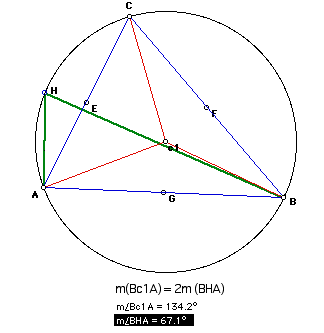Click HERE for a gsp sketch to see that the measurement of angle AHB will

stay the same as long as you stay on the "C" side of chord AB.

---

The length of segment AB is constant, thus m(Ac1B) is constant.

Now we can make the conclusion that

the locus of point C is the major arc of angle (Ac1B).

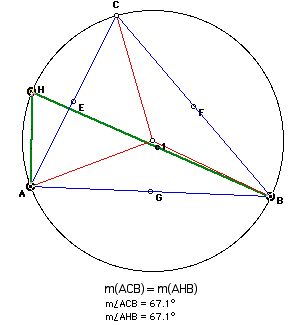If you are thirsty for more, try and figure out if anything special happens when point H dips below the chord.

If not, Click HERE to return to my homepage!