So, you really wanted
the proof. Well, here it is.
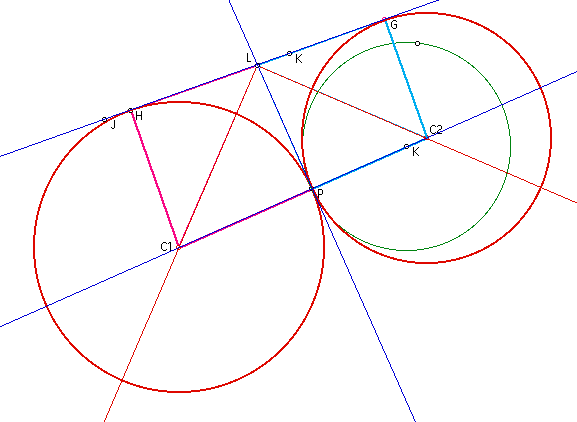
To begin with, I will
drop the perpendiculars from points C1 ans C2 to the given line
containing L.
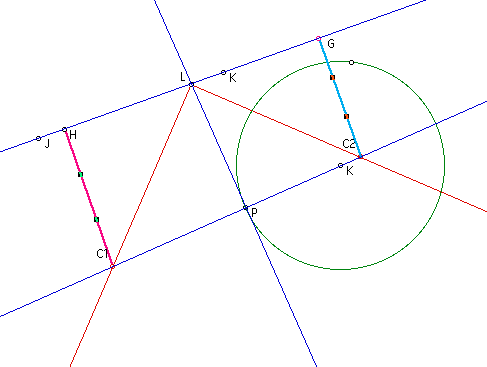
This is what that looks
like. Notice the pink and blue highlighted lines. The points where
the perpendiculars meet the given line have been labled H and
G.
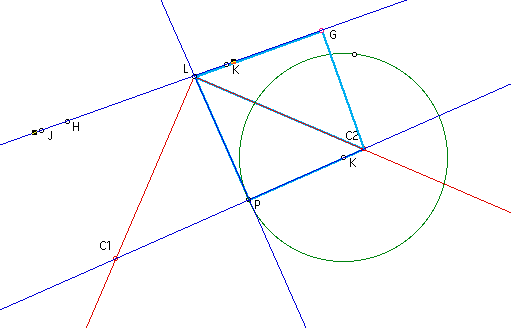
It is given that by constuction of
the angle bisector, that angles C2LG and C2LP are congruent.
By construction of the perpendiculars,
it holds that angles GLP and PC2G are right angles.
By the Triangle Sum Theorum, the angles
of a triangle equal 180 degrees, the angles LC2G and LC2P are
congruent.
Since LC2 is reflexive, we have that
triangles LGC2 and LPC2 are congruent by ASA congruency.
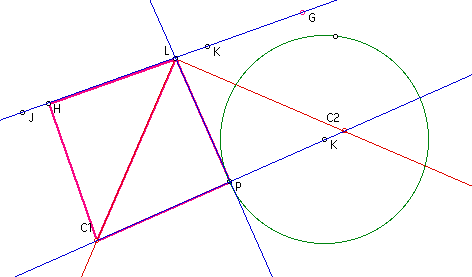
The same argument can be made for the
congruency of triangles LHC1 abd LPC1.
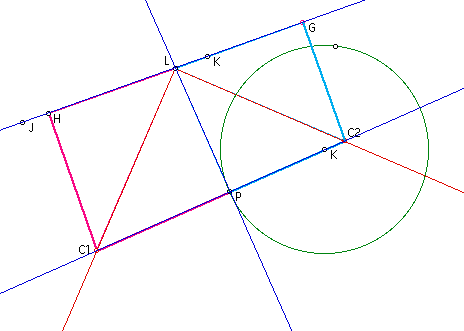
Since corresponding parts of a congruent
triangle are congruent, segments HC1 and PC1 are congruet, as
well as segments GC2 and PC2.
Since HC1 and PC1 are congruent, this
gives us that the center of the new circle is C1 with points H
and P on the circle.
Similarly, C2 is the center of the
other new circle with points G and P on the circle.
Because C1P and C2P are perpendicular
to line PL, and C1H and C2G are perpendicular to the given line,
the two constructed circles are tangent
to the given circle at point P and are tangent to the given line,
as required.
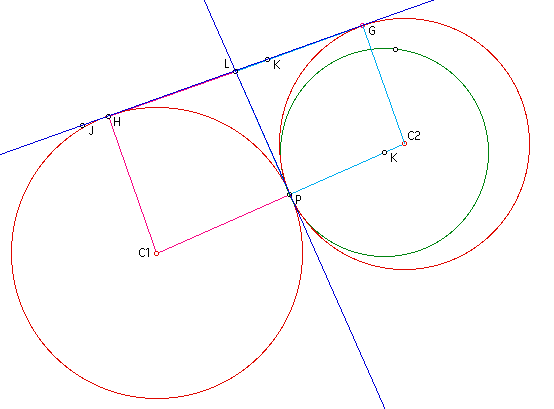
So, we have two circles both tangent
to a given circle and a given line.
 Return to
Investigation
Return to
Investigation






