Write Up 1

by

Alison Hays


Problem: Find two linear functions f(x) and g(x) such that their product

h(x) = f(x)*g(x)

is tangent to each of f(x) and g(x) at two distinct points.

(This is problem 3 of Assignment 1.)

Before solving this problem, let's look at the following:

Given two linear functions f(x) and g(x), explore, with different pairs of f(x) and g(x), the graphs for

h(x) = f(x)*g(x).

(This is part of problem 2 of Assignment 1.)

Let f(x) = ax + b, and let g(x) = cx + d.

Then h(x) = f(x) * g(x) = acx2 + adx + bcx + bd.

Suppose a = 1, b = 2, c = -3, and d = 4.

Then h(x) = -3x2 -2x + 8.

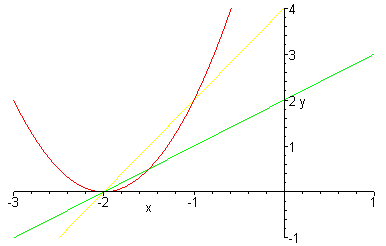
A plot of f(x), g(x), and h(x) is below.


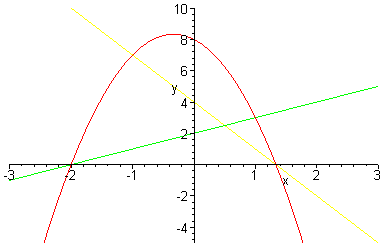
Notice that the roots of the parabola are the same as the roots of the two lines. In other words, the function f(x) = ax + b crosses the x-axis when f(x) = 0. Solving the equation 0 = ax + b for x, we see that x = -b/a. Therefore, the root of f(x) is -b/a.

Similarly, the root of g(x) is -d/c.

We see from the plot above that the roots of h(x) are -b/a and -d/c.

Are the roots of the parabola always the same as the roots of the lines, or is the previous example just a special case?

Recall how to find the roots of a quadratic function:

1. Factor the function:
          h(x) = (ax + b) * (cx + d).

2. Set each binomial equal to zero and solve for x:
          ax + b = 0 implies x = -b/a.
          cx + d = 0 implies x = -d/c.

Therefore, the roots of the quadratic function h(x) are the same as the roots on the linear functions f(x) and g(x).

Since the function h(x) is the product of two linear functions, we know that the parabola will have one or two real roots. It will have two roots if the roots of f and g are distinct. It will have one root if they are the same.

In the example above, the roots of the parabola are -2 and 4/3.

Where is the vertex of the parabola?

Recall that the x-coordinate of the vertex of a parabola with real roots is between the roots of the parabola. Therefore, the x-coordinate of the vertex of the parabola is

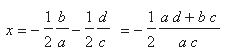
The y-coordinate of the vertex of the parabola, then, is

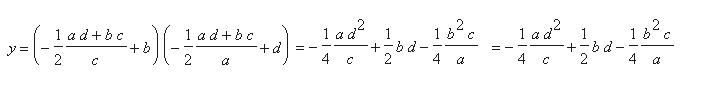
In the example above, the vertex of the parabola is the point (-1/3, 25/3).

Does the parabola "open up" or "open down"?

The concavity of the parabola depends only on the coefficient of the x2 term, ac. The parabola will open up if ac is positive, and it will open down if ac is negative. Therefore, it will open up if a and c have the same sign. It will open down if a and c have different signs.

In the example above, ac = -3, so the parabola opens down.

A few more examples...

Suppose a = 2, b = 3, c = 2, and d = 4. Then the roots of h are -3/2 and -2. The vertex of the parabola is the point (-7/4,-1/4), and the parabola opens up.

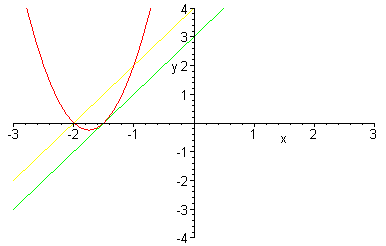
Suppose a = 1, b = 2, c = 2, and d = 4. Then h has one root of multiplicity 2: x = -2. The vertex of the parabola is the point (-2,0), and the parabola opens up.

Now let's go back to the original problem. Click here for my solution to the problem.

Alison's web page | Student Web Pages | EMAT 6680 Page